In this continuing series, we explore the NMath Stats functions for performing cluster analysis. (For previous posts, see Part 1 – PCA , Part 2 – K-Means, Part 3 – Hierarchical, and Part 4 – NMF.) The sample data set we’re using classifies 89 single malt scotch whiskies on a five-point scale (0-4) for 12 flavor characteristics. To visualize the data set and clusterings, we make use of the free Microsoft Chart Controls for .NET, which provide a basic set of charts.
In this post, the last in the series, we’ll look at how NMath provides a Monte Carlo method for performing multiple non-negative matrix factorization (NMF) clusterings using different random starting conditions, and combining the results.
NMF uses an iterative algorithm with random starting values for W and H. (See Part IV for more information on NMF.) This, coupled with the fact that the factorization is not unique, means that if you cluster the columns of V multiple times, you may get different final clusterings. The consensus matrix is a way to average multiple clusterings, to produce a probability estimate that any pair of columns will be clustered together.
To compute the consensus matrix, the columns of V are clustered using NMF n times. Each clustering yields a connectivity matrix. Recall that the connectivity matrix is a symmetric matrix whose i, jth entry is 1 if columns i and j of V are clustered together, and 0 if they are not. The consensus matrix is also a symmetric matrix, whose i, jth entry is formed by taking the average of the i, jth entries of the n connectivity matrices. The i, jth entry of a consensus matrix may be considered a “probability” that columns i and j belong to the same cluster.
NMath Stats provides class NMFConsensusMatrix for computing a consensus matrix. NMFConsensusMatrix is parameterized on the NMF update algorithm to use. Additional constructor parameters specify the matrix to factor, the order k of the NMF factorization (the number of columns in W), and the number of clustering runs. The consensus matrix is computed at construction time, so be aware that this may be an expensive operation.
For example, the following C# code creates a consensus matrix for 100 runs, clustering the scotch data (loaded into a dataframe in Part I) into four clusters:
int k = 4;
int numberOfRuns = 100;
NMFConsensusMatrix<NMFDivergenceUpdate> consensusMatrix =
new NMFConsensusMatrix<NMFDivergenceUpdate>(
data.ToDoubleMatrix().Transpose(),
k,
numberOfRuns);
Console.WriteLine("{0} runs out of {1} converged.",
consensusMatrix.NumberOfConvergedRuns, numberOfRuns);
The output is:
100 runs out of 100 converged.
NMFConsensusMatrix provides a standard indexer for getting the element value at a specified row and column in the consensus matrix. For instance, one of the goals of Young et al. was to identify single malts that are particularly good representatives of each cluster. This information could be used, for example, to purchase a representative sampling of scotches. As described in Part IV, they reported that these whiskies were the closest to each flavor profile:
- Glendronach and Macallan
- Tomatin and Speyburn
- AnCnoc and Miltonduff
- Ardbeg and Clynelish
The consensus matrix reveals, however, that the pairings are not equally strong:
Console.WriteLine("Probability that Glendronach is clustered with Macallan = {0}",
consensusMatrix[data.IndexOfKey("Glendronach"), data.IndexOfKey("Macallan")]);
Console.WriteLine("Probability that Tomatin is clustered with Speyburn = {0}",
consensusMatrix[data.IndexOfKey("Tomatin"), data.IndexOfKey("Speyburn")]);
Console.WriteLine("Probability that AnCnoc is clustered with Miltonduff = {0}",
consensusMatrix[data.IndexOfKey("AnCnoc"), data.IndexOfKey("Miltonduff")]);
Console.WriteLine("Probability that Ardbeg is clustered with Clynelish = {0}",
consensusMatrix[data.IndexOfKey("Ardbeg"), data.IndexOfKey("Clynelish")]);
The output is:
Probability that Glendronach is clustered with Macallan = 1 Probability that Tomatin is clustered with Speyburn = 0.4 Probability that AnCnoc is clustered with Miltonduff = 0.86 Probability that Ardbeg is clustered with Clynelish = 1
Thus, although Glendronach and Macallan are clustered together in all 100 runs, Tomatin and Speyburn are only clustered together 40% of the time.
A consensus matrix, C, can itself be used to cluster objects, by perform a hierarchical cluster analysis using the distance function:
![]()
For example, this C# code creates an hierarchical cluster analysis using this distance function, then cuts the tree at the level of four clusters, printing out the cluster members:
DoubleMatrix colNumbers = new DoubleMatrix(consensusMatrix.Order, 1, 0, 1);
string[] names = data.StringRowKeys;
Distance.Function distance =
delegate(DoubleVector data1, DoubleVector data2)
{
int i = (int)data1[0];
int j = (int)data2[0];
return 1.0 - consensusMatrix[i, j];
};
ClusterAnalysis ca = new ClusterAnalysis(colNumbers, distance, Linkage.WardFunction);
int k = 4;
ClusterSet cs = ca.CutTree(k);
for (int clusterNumber = 0; clusterNumber < cs.NumberOfClusters; clusterNumber++)
{
int[] members = cs.Cluster(clusterNumber);
Console.Write("Objects in cluster {0}: ", clusterNumber);
for (int i = 0; i < members.Length; i++)
{
Console.Write("{0} ", names[members[i]]);
}
Console.WriteLine("\n");
}
The output is:
Objects in cluster 0: Aberfeldy Auchroisk Balmenach Dailuaine Glendronach Glendullan Glenfarclas Glenrothes Glenturret Macallan Mortlach RoyalLochnagar Tomore Objects in cluster 1: Aberlour ArranIsleOf Belvenie BenNevis Benriach Benromach Bladnoch BlairAthol Bowmore Craigallechie Dalmore Dalwhinnie Deanston GlenElgin GlenGarioch GlenKeith GlenOrd Glenkinchie Glenlivet Glenlossie Inchgower Knochando Linkwood OldFettercairn RoyalBrackla Speyburn Teaninich Tomatin Tomintoul Tullibardine Objects in cluster 2: AnCnoc Ardmore Auchentoshan Aultmore Benrinnes Bunnahabhain Cardhu Craigganmore Dufftown Edradour GlenGrant GlenMoray GlenSpey Glenallachie Glenfiddich Glengoyne Glenmorangie Loch Lomond Longmorn Mannochmore Miltonduff Scapa Speyside Strathisla Strathmill Tamdhu Tamnavulin Tobermory Objects in cluster 3: Ardbeg Balblair Bruichladdich Caol Ila Clynelish GlenDeveronMacduff GlenScotia Highland Park Isle of Jura Lagavulin Laphroig Oban OldPulteney Springbank Talisker
Once again using the cluster assignments to color the objects in the plane of the first two principal components, we can see the grouping represented by the consensus matrix (k=4).
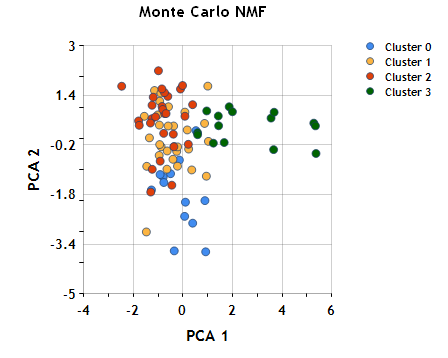
Well, this concludes are tour through the NMath clustering functionality. Techniques such as principal component analysis, k-means clustering, hierarchical cluster analysis, and non-negative matrix factorization can all be applied to data such as these to explore various clusterings. Choosing among these approaches is ultimately a matter of domain knowledge and performance requirements. Is it appropriate to cluster based on distance in the original space, or should dimension reduction be applied? If dimension reduction is used, are negative component parameters meaningful? Are there sufficient computational resource available to construct a complete hierarchical cluster tree, or should a k-means approach be used? If an hierarchical cluster tree is computed, what distance and linkage function should be used? NMath provides a powerful, flexible set of clustering tools for data mining and data analysis.
Ken
References
Young, S.S., Fogel, P., Hawkins, D. M. (unpublished manuscript). “Clustering Scotch Whiskies using Non-Negative Matrix Factorization”. Retrieved December 15, 2009 from http://niss.org/sites/default/files/ScotchWhisky.pdf.
