In this continuing series, we explore the NMath Stats functions for performing cluster analysis. (For previous posts, see Part 1 – PCA , Part 2 – K-Means, and Part 3 – Hierarchical.) The sample data set we’re using classifies 89 single malt scotch whiskies on a five-point scale (0-4) for 12 flavor characteristics. To visualize the data set and clusterings, we make use of the free Microsoft Chart Controls for .NET, which provide a basic set of charts.
In this post, we’ll cluster the scotches using non-negative matrix factorization (NMF). NMF approximately factors a matrix V into two matrices, W and H:
![]()
If V in an n x m matrix, then NMF can be used to approximately factor V into an n x r matrix W and an r x m matrix H. Usually r is chosen to be much smaller than either m or n, for dimension reduction. Thus, each column of V is approximated by a linear combination of the columns of W, with the coefficients being the corresponding column H. This extracts underlying features of the data as basis vectors in W, which can then be used for identification, clustering, and compression.
Earlier in this series, we used principal component analysis (PCA) as a means of dimension reduction for the purposes of visualizing the scotch data. NMF differs from PCA in two important respects:
- NMF enforces the constraint that the factors W and H must be non-negative-that is, all elements must be equal to or greater than zero. By not allowing negative entries in W and H, NMF enables a non-subtractive combination of the parts to form a whole, and in some contexts, more meaningful basis vectors. In the scotch data, for example, what would it mean for a scotch to have a negative value for a flavor charactistic?
- NMF does not require the basis vectors to be orthogonal. If we are using NMF to extract meaningful underlying components of the data, there is no a priori reason to require the components to be orthogonal.
Let’s begin by reproducing the NMF analysis of the scotch data presented in Young et al.. The authors performed NMF with r=4, to identify four major flavor factors in scotch whiskies, and then asked whether there are single malts that appear to be relatively pure embodiments of these four flavor profiles.
NMath Stats provides class NMFClustering for performing data clustering using iterative nonnegative matrix factorization (NMF), where each iteration step produces a new W and H. At each iteration, each column v of V is placed into a cluster corresponding to the column w of W which has the largest coefficient in H. That is, column v of V is placed in cluster i if the entry hij in H is the largest entry in column hj of H. Results are returned as an adjacency matrix whose i, jth value is 1 if columns i and j of V are in the same cluster, and 0 if they are not. Iteration stops when the clustering of the columns of the matrix V stabilizes.
NMFClustering is parameterized on the NMF update algorithm to use. For instance:
NMFClustering<NMFDivergenceUpdate> nmf = new NMFClustering<NMFDivergenceUpdate>();
This specifies the divergence update algorithm, which minimizes a divergence functional related to the Poisson likelihood of generating V from W and H. (For more information, see Brunet, Jean-Philippe et al. , 2004.)
The Factor() method performs the actual iterative factorization. The following C# code clusters the scotch data (loaded into a dataframe in Part I) into four clusters:
int k = 4;
// specify starting conditions (optional)
int seed = 1973;
RandGenUniform rnd = new RandGenUniform(seed);
DoubleMatrix starting_W = new DoubleMatrix(data.Cols, k, rnd);
DoubleMatrix starting_H = new DoubleMatrix(k, data.Rows, rnd);
nmf.Factor(data.ToDoubleMatrix().Transpose(),
k,
starting_W,
starting_H);
Console.WriteLine("Factorization converged in {0} iterations.\n",
nmf.Iterations);
There are a couple things to note in this code:
- By default, NMFact uses random starting values for W and H. This, coupled with the fact that the factorization is not unique, means that if you cluster the columns of V multiple times, you may get different final clusterings. In order to reproduce the results in Young et al. the code above specifies a particular random seed for the initial conditions.
- The scotch data needs to be transposed before clustering, since NMFClustering requires each object to be clustered to be a column in the input matrix.
The output is:
Factorization converged in 530 iterations.
We can examine the four flavor factors (columns of W) to see what linear combination of the original flavor characteristics each represents. The following code orders each factor, normalized so the largest value is 1.0, similar to the data shown in Table 1 of Young et al.:
ReproduceTable1(nmf.W, data.ColumnHeaders);
private static void ReproduceTable1(DoubleMatrix W,
object[] rowKeys)
{
// normalize
for (int i = 0; i < W.Cols; i++)
{
W[Slice.All, i] /= NMathFunctions.MaxValue(W.Col(i));
}
// Create data frame to hold W
string[] factorNames = GetFactorNames(W.Cols);
DataFrame df_W = new DataFrame(W, factorNames);
df_W.SetRowKeys(rowKeys);
// Print out sorted columns
for (int i = 0; i < df_W.Cols; i++)
{
df_W.SortRows(new int[] { i },
new SortingType[] { SortingType.Descending });
Console.WriteLine(df_W[Slice.All, new Slice(i, 1)]);
Console.WriteLine();
}
Console.WriteLine();
}
The output is:
# Factor 0 Fruity 1.0000 Floral 0.8681 Sweetness 0.8292 Malty 0.6568 Nutty 0.5855 Body 0.4295 Smoky 0.2805 Honey 0.2395 Spicy 0.0000 Winey 0.0000 Tobacco 0.0000 Medicinal 0.0000 # Factor 1 Winey 1.0000 Body 0.6951 Nutty 0.5078 Sweetness 0.4257 Honey 0.3517 Malty 0.3301 Fruity 0.2949 Smoky 0.2631 Spicy 0.0000 Floral 0.0000 Tobacco 0.0000 Medicinal 0.0000 # Factor 2 Spicy 1.0000 Honey 0.4885 Sweetness 0.4697 Floral 0.4301 Smoky 0.3508 Malty 0.3492 Body 0.3160 Fruity 0.0036 Nutty 0.0000 Winey 0.0000 Tobacco 0.0000 Medicinal 0.0000 # Factor 3 Medicinal 1.0000 Smoky 0.8816 Body 0.7873 Spicy 0.3936 Sweetness 0.3375 Malty 0.3069 Nutty 0.2983 Fruity 0.2441 Tobacco 0.2128 Floral 0.0000 Winey 0.0000 Honey 0.0000
Thus:
- Factor 0 contains Fruity, Floral, and Sweetness flavors.
- Factor 1 emphasizes the Winey flavor.
- Factor 2 contains Spicy and Honey flavors.
- Factor 3 contains Medicinal and Smokey flavors.
The objects are placed into clusters corresponding to the column of W which has the largest coefficient in H. The following C# code prints out the contents of each cluster, ordered by largest coefficient, after normalizing so the sum of each component is 1.0:
ReproduceTable2(nmf.H, data.RowKeys, nmf.ClusterSet);
private static void ReproduceTable2(DoubleMatrix H, object[] rowKeys, ClusterSet cs)
{
// normalize
for (int i = 0; i < H.Rows; i++)
{
H[i, Slice.All] /= NMathFunctions.Sum(H.Row(i));
}
// Create data frame to hold H
string[] factorNames = GetFactorNames(H.Rows);
DataFrame df_H = new DataFrame(H.Transpose(), factorNames);
df_H.SetRowKeys(rowKeys);
// Print information on each cluster
for (int clusterNumber = 0; clusterNumber < cs.NumberOfClusters; clusterNumber++)
{
int[] members = cs.Cluster(clusterNumber);
int factor = NMathFunctions.MaxIndex(H.Col(members[0]));
Console.WriteLine("Cluster {0} ordered by {1}: ", clusterNumber, factorNames[factor]);
DataFrame cluster = df_H[new Subset(members), Slice.All];
cluster.SortRows(new int[] { factor }, new SortingType[] { SortingType.Descending });
Console.WriteLine(cluster);
Console.WriteLine();
}
}
The output is:
Cluster 0 ordered by Factor 1: # Factor 0 Factor 1 Factor 2 Factor 3 Glendronach 0.0000 0.0567 0.0075 0.0000 Macallan 0.0085 0.0469 0.0083 0.0000 Balmenach 0.0068 0.0395 0.0123 0.0000 Dailuaine 0.0070 0.0317 0.0164 0.0000 Mortlach 0.0060 0.0316 0.0240 0.0000 Tomore 0.0000 0.0308 0.0000 0.0000 RoyalLochnagar 0.0104 0.0287 0.0164 0.0000 Glenrothes 0.0054 0.0280 0.0081 0.0000 Glenfarclas 0.0127 0.0279 0.0164 0.0000 Auchroisk 0.0103 0.0267 0.0099 0.0000 Aberfeldy 0.0125 0.0238 0.0117 0.0000 Strathisla 0.0162 0.0229 0.0151 0.0000 Glendullan 0.0140 0.0228 0.0102 0.0000 BlairAthol 0.0111 0.0211 0.0166 0.0000 Dalmore 0.0088 0.0208 0.0114 0.0204 Ardmore 0.0104 0.0182 0.0118 0.0000 Cluster 1 ordered by Factor 2: # Factor 0 Factor 1 Factor 2 Factor 3 Tomatin 0.0000 0.0170 0.0306 0.0000 Aberlour 0.0136 0.0260 0.0282 0.0000 Belvenie 0.0087 0.0123 0.0262 0.0000 GlenGarioch 0.0079 0.0086 0.0252 0.0000 Speyburn 0.0115 0.0000 0.0244 0.0000 BenNevis 0.0202 0.0000 0.0242 0.0000 Bowmore 0.0049 0.0109 0.0225 0.0186 Inchgower 0.0104 0.0000 0.0218 0.0118 Craigallechie 0.0131 0.0098 0.0216 0.0136 Tomintoul 0.0085 0.0083 0.0214 0.0000 Benriach 0.0150 0.0000 0.0214 0.0000 Glenlivet 0.0125 0.0176 0.0205 0.0000 Glenturret 0.0080 0.0228 0.0203 0.0000 Benromach 0.0132 0.0140 0.0198 0.0000 Glenkinchie 0.0112 0.0000 0.0190 0.0000 OldFettercairn 0.0068 0.0137 0.0182 0.0160 Knochando 0.0131 0.0133 0.0179 0.0000 GlenOrd 0.0118 0.0128 0.0175 0.0000 Glenlossie 0.0143 0.0000 0.0167 0.0000 GlenDeveronMacduff 0.0000 0.0156 0.0158 0.0216 GlenKeith 0.0108 0.0146 0.0145 0.0000 ArranIsleOf 0.0073 0.0086 0.0127 0.0125 GlenSpey 0.0086 0.0091 0.0119 0.0000 Cluster 2 ordered by Factor 0: # Factor 0 Factor 1 Factor 2 Factor 3 AnCnoc 0.0294 0.0000 0.0000 0.0000 Miltonduff 0.0242 0.0000 0.0000 0.0000 Aultmore 0.0242 0.0000 0.0000 0.0000 Longmorn 0.0214 0.0141 0.0089 0.0000 Cardhu 0.0204 0.0000 0.0094 0.0000 Auchentoshan 0.0203 0.0000 0.0065 0.0000 Strathmill 0.0203 0.0000 0.0125 0.0000 Edradour 0.0195 0.0172 0.0092 0.0000 Tobermory 0.0190 0.0000 0.0000 0.0000 Glenfiddich 0.0190 0.0000 0.0000 0.0000 Tamnavulin 0.0189 0.0000 0.0148 0.0000 Dufftown 0.0189 0.0000 0.0000 0.0147 Craigganmore 0.0184 0.0000 0.0030 0.0254 Speyside 0.0182 0.0138 0.0000 0.0000 Glenallachie 0.0178 0.0000 0.0108 0.0000 Dalwhinnie 0.0174 0.0000 0.0172 0.0000 GlenMoray 0.0174 0.0079 0.0157 0.0000 Tamdhu 0.0172 0.0124 0.0000 0.0000 Glengoyne 0.0170 0.0090 0.0065 0.0000 Benrinnes 0.0158 0.0196 0.0161 0.0000 GlenElgin 0.0155 0.0107 0.0133 0.0000 Bunnahabhain 0.0148 0.0075 0.0078 0.0110 Glenmorangie 0.0143 0.0000 0.0123 0.0166 Scapa 0.0140 0.0128 0.0089 0.0127 Bladnoch 0.0137 0.0063 0.0088 0.0000 Linkwood 0.0129 0.0165 0.0092 0.0000 Mannochmore 0.0124 0.0126 0.0081 0.0000 GlenGrant 0.0122 0.0121 0.0000 0.0000 Deanston 0.0119 0.0151 0.0122 0.0000 Loch Lomond 0.0105 0.0000 0.0094 0.0130 Tullibardine 0.0099 0.0093 0.0098 0.0138 Cluster 3 ordered by Factor 3: # Factor 0 Factor 1 Factor 2 Factor 3 Ardbeg 0.0000 0.0000 0.0000 0.0906 Clynelish 0.0001 0.0000 0.0000 0.0855 Lagavulin 0.0000 0.0138 0.0000 0.0740 Laphroig 0.0000 0.0082 0.0000 0.0731 Talisker 0.0030 0.0000 0.0129 0.0706 Caol Ila 0.0048 0.0000 0.0019 0.0694 Oban 0.0067 0.0000 0.0008 0.0564 OldPulteney 0.0114 0.0073 0.0000 0.0429 Isle of Jura 0.0079 0.0000 0.0059 0.0352 Balblair 0.0125 0.0000 0.0074 0.0297 Springbank 0.0000 0.0142 0.0189 0.0282 RoyalBrackla 0.0122 0.0078 0.0135 0.0276 GlenScotia 0.0096 0.0144 0.0000 0.0275 Bruichladdich 0.0100 0.0098 0.0140 0.0249 Teaninich 0.0081 0.0000 0.0111 0.0216 Highland Park 0.0050 0.0145 0.0146 0.0211
These data are very similar to those shown in Table 2 in Young et al. According to their analysis, the most representative malts in each cluster are:
- Glendronach and Macallan
- Tomatin and Speyburn
- AnCnoc and Miltonduff
- Ardbeg and Clynelish
As you can see, these scotches are at, or very near, the top of each ordered cluster in the output above.
Finally, it is interesting to view the clusters found by NMF in the same plane of the first two principal components that we have looked at previously.
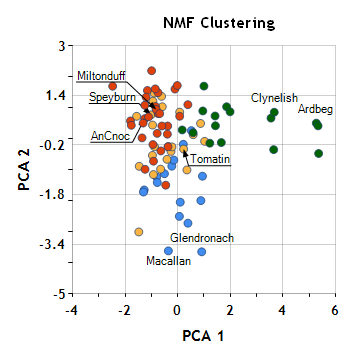
If you compare this plot to that produced by k-means clustering or hierarchical cluster analysis, you can see how different the results are. We are no longer clustering based on “similarity” in the original 12-dimensional flavor space (of which this is a view). Instead, we’ve used a reduced set of synthetic dimensions which capture underlying features in the data.
In order to produce results similar to those of Young et al. we explicitly specified a random seed to the NMF process. With different seeds, somewhat different final clusterings can occur. In the final post in this series, we’ll look at how NMath provides a Monte Carlo method for performing multiple NMF clusterings using different random starting conditions, and combining the results.
Ken
References
Brunet, Jean-Philippe et al. (2004). “Metagenes and Molecular Pattern Discovery Using Matrix Factorization”, Proceedings of the National Academy of Sciences 101, no. 12 (March 23, 2004): 4164-4169.
Young, S.S., Fogel, P., Hawkins, D. M. (unpublished manuscript). “Clustering Scotch Whiskies using Non-Negative Matrix Factorization”. Retrieved December 15, 2009 from http://niss.org/sites/default/files/ScotchWhisky.pdf.

One thought on “Cluster Analysis, Part IV: Non-negative Matrix Factorization (NMF)”