Searching for Roots in Univariate Functions

Finding the roots of a univariate function is a basic numerical procedure that nearly all engineers and scientists encounters at some point, because the root finding question addresses the basic equation,

where, x can be a real or complex variable. Or more generally, we can solve,

by finding the roots to,

Algorithms

I will demonstrate three well known univariate root finding algorithms, Newton-Raphson, Ridders, and Secant. All three methods require a delegate to the function and a bracketed range where a root is expected to reside, additionally, Newton-Raphson requires a continuous, non-zero derivative of f(x)in the region of the root. None of these methods are recommended for finding roots of polynomials in general, although Newton-Raphson will work well if the polynomial isn’t ill-conditioned by containing an even number of duplicated roots (Bracketing such roots isn’t possible because the function doesn’t change sign in the region of these roots.), or by containing root pairs extremely close together.

Name	Convergence Rate	Root remains bracketed?	Comments
Newton-Raphson	Quadratic	Yes	Often used for root polishing.
Secant	Golden Ration – 1.618	No	Fast in locally linear regions.
Ridders	Quadratic	Yes	Frequently competitive with the more complex Brent’s method

C# Example with NMath

All of these roots finders have a similar interface and properties in NMath, so exchanging one with the other is easy. As seen in the example below, both the Ridders and Secant root finders implement the IOneVariableRootFinder interface, and the Newton-Raphson root finder implements the slightly different IOneVariableDRootFinder, where the ‘D’ stands for derivative.

Using Wolfram|Alpha’s online services, I’ve computed and graphed the roots of the following non-linear univariate function.

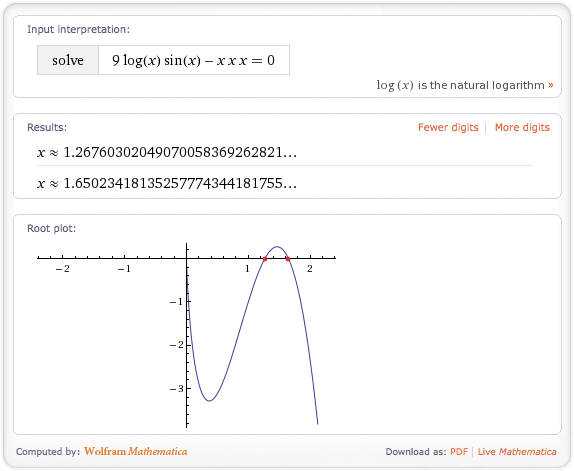
The code block below demonstrates the use of each of these root finders, and shows the how to define a function delegate using a lamda expression. I find lamda expressions are convenient for defining delegates to mathematical expressions and that they create very readable code. (As an aside, lamda expressions are a C# language feature, and are not part of the .NET framework. Therefore, applications targeting the .NET 2.0 framework can leverage lamda expressions as long as the compiler supports them, as VS9 and VS10 both do.).

using CenterSpace.NMath.Analysis;

void RootFindingExample()
    {
  
     // Create the function delegate with a lamda expression, 
     // and the interval which contains a root.
      OneVariableFunction f = 
        new OneVariableFunction(x => 9 * Math.Log(x) * Math.Sin(x) - x * x * x);
      Interval bracket = new Interval(1, 1.5, Interval.Type.Closed);

      IOneVariableDRootFinder nrRoots = new NewtonRaphsonRootFinder(3);
      Double rootnewton = nrRoots.Find(f, f.Derivative(), bracket);
      Console.WriteLine(String.Format("Newton-Raphson root is = {0}", rootnewton));

      IOneVariableRootFinder rootFinder = new RiddersRootFinder(3);
      Double rootridder = rootFinder.Find(f, bracket);
      Console.WriteLine(String.Format("Ridder's root is = {0}", rootridder));

      rootFinder = new SecantRootFinder(3);
      Double rootsecant = rootFinder.Find(f, bracket);
      Console.WriteLine(String.Format("Secant root is = {0}", rootsecant));

    }

With each root finder limited to just 3 iterations, this program creates the output,

Newton-Raphson root is = 1.26760302048967
Ridder's root is = 1.26760302063032
Secant root is = 1.3334994219432

Where Newton-Raphson found the first root most accurately with it’s knowledge of derivative information. Besides specifying the maximum number of iterations, a root tolerance can also be used to control convergence effort.

A second somewhat more difficult example which can cause problems for both the Secant and Newton-Raphson methods.

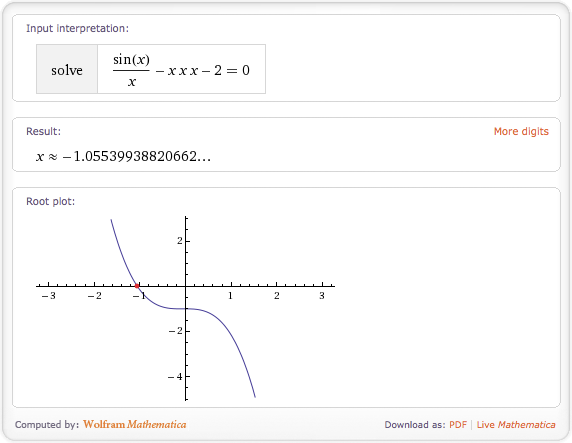
I gave the Secant method 1000 iterations, and still it’s root estimate was very poor – in fact with an initial bracket of [-5, -0.01], the Secant method will never converge on the root. There is a stable orbit around which the Secant method spins forever, preventing convergence. Because the Newton-Raphson requires a continuous derivative any starting bracket that contains the origin will cause an exception to be thrown because of the discontinuous derivative at zero.

Newton-Raphson root is = -1.05539938820662 (with 8 iterations)
Ridder's root is = -1.05539938548287 (with 8 iterations)
Secant root is = -0.0912954387917323 (with 1000 iterations)

As a general recommendation, I would start my root search using Ridder’s method and then finish up by polishing with Newton-Raphson.

-Happy Computing,
Paul