Chebyshev Filters in C#

There are three classes of widely used IIR (recursive) filters in signal processing: Butterworth, Chebyshev, and elliptical. In this postI will give a short introduction to Chebyshev filters, present a code implementation, and end with a usage example. The Butterworth filter was discussed in a previous blog article.

Chebyshev filters come in two flavors defined by either allowing ripple in the pass-band (type 1) or ripple the stop-band (type 2). We will only discuss the type 1 filters here, as the type 2 filters are rarely used. Type 1 Chebyshev filters trade-off steeper roll-off with ripple in the pass band and in the limit of zero ripple, mimic Butterworth filters. Simply put, the more ripple allowed in the passband, the steep roll-off the filter achieves.
Chebyshev filters derive their name from Chebyshev polynomials [1]. Finding Chebyshev polynomials for a given order represent a computational challenge, and when computed often exhibit various numerical instabilities (often overflow) if not done properly. For an excellent review and comparison of computational techniques for computing Chebyshev polynomials see this paper by Wolfram Koepf. Here, we will side step the entire computational issue, as legions of engineers have done before us, and simply look up the Chebyshev polynomials, by order, in a switch statement. Because Chebyshev filters with an order n above 10 or 12 would be unusual, this table look-up approach can be considered, practically speaking, complete.

Wikipedia has a excellent overview article discussing the Chebyshev filter, so I’ll refer you there for a background treatment of Chebyshev filtering theory.

Chebyshev Filters

The gain expression for Chebyshev filters has a very similar structure to Butterworth filters. As with the Butterworth filter, there are the three familiar design parameters, DC Gain, cutoff frequency f0, and filter order n, with an additional parameter, epsilon, for specifying the desired pass-band ripple.

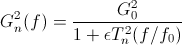
The Tn signifies a Chebyshev polynomial of order n. So for example when n = 2, it happens that Tn = 2*x*x - 1, where when substituted into the gain equation we replace x with f/f0. The ripple factor can be equated to pass-band ripple in Db with the equation:

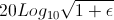
Typical values for epsilon would range between 0.1 and 1.

The Chebyshev Filter in Code

We take the identical approach to implementing the Chebyshev filter in code as we did with the Butterworth filter. We will first compute the input signal’s FFT, then multiply that by the above filter gain, and then take the inverse FFT of that product resulting in our filtered signal. This is a O( n*log(n)) operation.

But before we do that, we need a way to find the Chebyshev polynomials of a given order n. To that end I’ve build a simple method that returns a Chebyshev polynomial given the order; if the requested order is larger than the look-up table, a NotImplementedException is thrown. This look-up approach can easily be extended as far as would be needed for most any practicable Chebyshev filter.

Chebyshev Polynomial Lookup

 private Polynomial ChebyshevPolynomial( int order)
    {
      switch( order )
      {
        case 0:
          return new Polynomial( new DoubleVector( "1" ) );
        case 1:
          return new Polynomial( new DoubleVector( "0 1" ) );
        case 2:
          return new Polynomial( new DoubleVector( "-1 0 2" ) );
        case 3:
          return new Polynomial( new DoubleVector( "0 -3 0 4" ) );
        case 4:
          return new Polynomial( new DoubleVector( "1 0 -8 0 8" ) );
        case 5:
          return new Polynomial( new DoubleVector( "0 5 0 -20 0 16" ) );
        case 6:
          return new Polynomial( new DoubleVector( "-1 0 18 0 -48 0 32" ) );
        case 7:
          return new Polynomial( new DoubleVector( "0 7 0 56 0 -112 0 64" ) );
        case 8:
          return new Polynomial( new DoubleVector( "1 0 -32 0 160 0 -256 0 128" ) );
        default:
          throw new NotImplementedException();     
      }
   }

An excellent on-line resource for Chebyshev polynomials, or any other integer sequence can be found at OEIS, the Online Encyclopaedia of Integer Sequences. If you wish to delve into computing the coefficients of Chebyshev polynomials, a good review of techniques can be found here.

Chebyshev Filter

The following code implements the Chebyshev filter, following the three steps mentioned above: [1] FFT(signal), [2] FFT(signal)*G(f), [3] IFFT.

private DoubleComplexVector ChebeshevFilter( DoubleComplexVector signal, 
  double sampleFrequency, int order, double f0, 
  double ripple, double DCGain )
    {
      // Get the Chebyshev polynomial
      Polynomial T = ChebyshevPolynomial( order );

      int N = signal.Length;

      // Apply forward FFT in place
      DoubleComplexForward1DFFT fft = new DoubleComplexForward1DFFT( N );
      DoubleComplexVector signalFFT = fft.FFT( signal );

      // Remove DC offset
      signalFFT[0] = 0;

      if ( f0 > 0 )
      {

        double numBins = N / 2;  // Half the length of the FFT by symmetry
        double binWidth = sampleFrequency / numBins; // Hz

        // Filter
        System.Threading.Tasks.Parallel.For( 1, N / 2, i =>
        {
          double binFreq = binWidth * i;
          double gain = 
            DCGain / ( Math.Sqrt( ( 1 + ripple * Math.Pow( T.Evaluate( binFreq / f0) , 2.0 ) ) ) );
          signalFFT[i] *= gain;
          signalFFT[N - i] *= gain;
        } );

      }

      // Reverse filtered signal
      DoubleComplexBackward1DFFT ifft = new DoubleComplexBackward1DFFT( N );
      ifft.SetScaleFactorByLength(); // Needed to get the correct amplitude
      signal = ifft.FFT( signalFFT );

      return signal;
    }

Filtering Example

To test the Chebyshev filtering code above, I’ve generated a test signal which is the sum to two sinusoids of frequences 1 Hz and 8 Hz. For comparison, this is the same test signal I used to test the Butterworth filter in my previous post. The test signal is sampled at 25 Hz and then filtered using a third order Chebyshev filter with a frequency cut-off of 1.5 Hz and ripple factor (epsilon) of 0.2.

public void ChebyshevFilterTest()
    {
      DoubleComplexVector signal = new DoubleComplexVector( 100 );

      double Fs = 25; // Sample rate, 25Hz
      double f1 = 1; // 1 Hz Signal
      double f2 = 8; // 8 Hz Signal
      for ( int t = 0; t < 100; t++ )
      {
        signal[t] = new DoubleComplex( Math.Sin( 2 * Math.PI * f1 / Fs * t ) + Math.Sin( 2 * Math.PI * f2 / Fs * t ), 0.0 );
      }

      // Filter      
      DoubleComplexVector filteredSignal = this.ChebeshevFilter( signal, 25, 3, 1.5, 0.2, 1.0 );

      // Display results
      Chart chart = NMathChart.ToChart( new DoubleVector( signal.ToRealDataTable() ) );
      chart.Titles[0].Text = "Input signal, sampled at 25 Hz";
      chart.ChartAreas[0].AxisY.Title = "Input signal magnitude";
      chart.ChartAreas[0].AxisX.Minimum = 0;
      Chart chartfft = NMathChart.ToChart( new DoubleVector( filteredSignal.ToRealDataTable() ) );
      chartfft.Titles[0].Text = "Filtered signal";
      chartfft.ChartAreas[0].AxisY.Title = "Filtered signal magnitude";
      chartfft.ChartAreas[0].AxisX.Minimum = 0;

      List charts = new List() { chart, chartfft };

      Chart compositeChart = NMathChart.Compose( charts, 1, 2, NMathChart.AreaLayoutOrder.ColumnMajor );
      compositeChart.Width = 650;
      compositeChart.Height = 300;

      NMathChart.Show( compositeChart );

    }

This example test code, using NMath charts, generates the following chart of the unfiltered and filtered signal side by side.

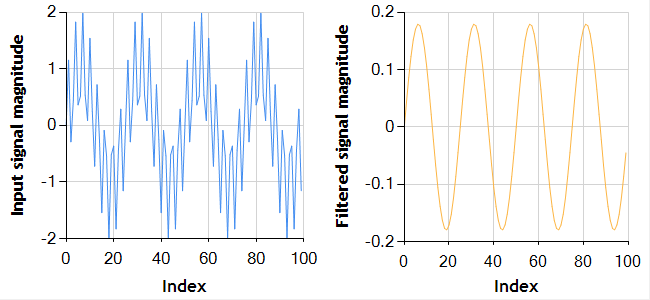
-Happy Computing,

Paul

[1] Chebyshev is a transliteration of a Russian name and in the past has been variously spelled as Chebychev, Tschebyscheff, Tchebysheff and Tchebichef.