NMath Premium is our new GPU-accelerated math and statistics library for the .NET platform. The supported NVIDIA GPU routines include both a range of dense linear algebra algorithms and 1D and 2D Fast Fourier Transforms (FFTs). NMath Premium is designed to be a near drop-in replacement for NMath, however there are a few important differences and additional logging capabilities that are specific to the premium product.
NMath Premium will be released June 11. For immediate access, sign up here to join the beta program.
Benchmark Approach
Modern FFT implementations are hybridized algorithms which switch between algorithmic approaches and processing kernels depending on the available hardware, FFT type, and FFT length. A FFT library may use the straight Cooly-Tukey algorithm for a short power-of-two FFT but switch to Bluestein’s algorithm for odd-length FFT’s. Further, depending on the factors of the FFT length different combinations of processing kernels may be used. In other words there is no single ‘FFT algorithm’ and so there is no easy expression for FLOPS completed per FFT computed. Therefore, when analyzing the performance of FFT libraries today, the performance is often reported relative to the Cooly-Tukey implementation with the FLOPs estimated at 5 * N * log( N ) . This relative performance is reported here. As an example, if we report a performance of 10 GFLOP’s for a particular FFT, that means if you ran an implementation of the Cooly-Tukey algorithm you’d need a 10 GFLOP’s capable machine to match the performance (finish as quickly).
Because GPU computation takes place in a different memory space from the CPU, all data must be copied to the GPU and the results then copied back to the CPU. This copy time overhead is included in all reported performance numbers. We include this copy time to give our library users an accurate picture of attainable performance.
GPU’s Tested
The NMath Premium 1D and 2D FFT library was tested on four different NVIDIA GPU’s and a 4-core 2.0Ghz Intel i7. These models represent the current range of performance available from NVIDIA, ranging from the widely installed GeForce GTX 525 to NVIDIA’s fasted double precision GPU, the Tesla K20.
| GPU | Peak GFLOP (single / double) | Summary |
|---|---|---|
| Tesla K20 | 3510 / 1170 | Optimized for applications requiring double precision performance such as computational physics, biochemistry simulations, and computational finance. |
| Tesla K10 | 2288/ 95 | This is a dual GPU processor card optimized for single precision performance for applications such as seismic and video or image processing. If both GPU cores are maximally utilized these GFLOP numbers would double. |
| Tesla 2090 | 1331/ 655 | A single core GPU with a more balanced single and double precision performance. |
| GeForce 525 | 230 / – | A single core consumer GPU found in many gaming computers. |
FFT Performance Charts
The four charts below represent the performance of various power-of-two length, complex to complex forward 1D and 2D FFT’s. All NMath products also seamlessly compute non-power-of-two length FFT’s but their performance is not part of this GPU comparison note.
The performance of the CPU-bound 1D FFT outperformed all of the GPU’s for relatively short FFT lengths. This is expected because the superior performance of the GPU’s cannot be enjoyed due to the data transfer overhead. Once the computational complexity of the 1D FFT is high enough the data transfer overhead is outweighed by the efficient parallel nature of the GPU’s, and they start to overtake the CPU-bound 1D FFT’s. This cross-over point occurs when the FFT reaches a length near 65536. The exception is the consumer level GeForce GTX 525, where the GPU and CPU FFT performance roughly track each other.
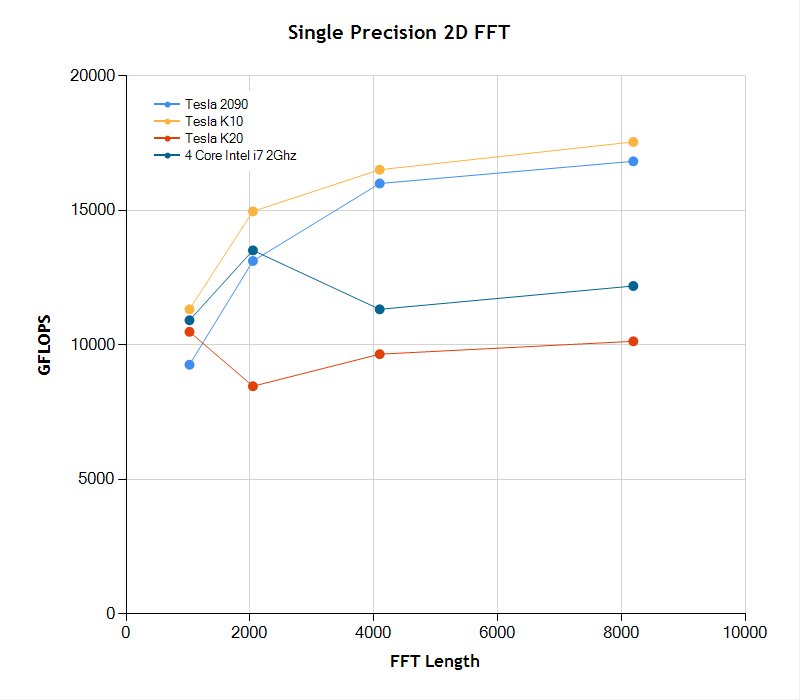
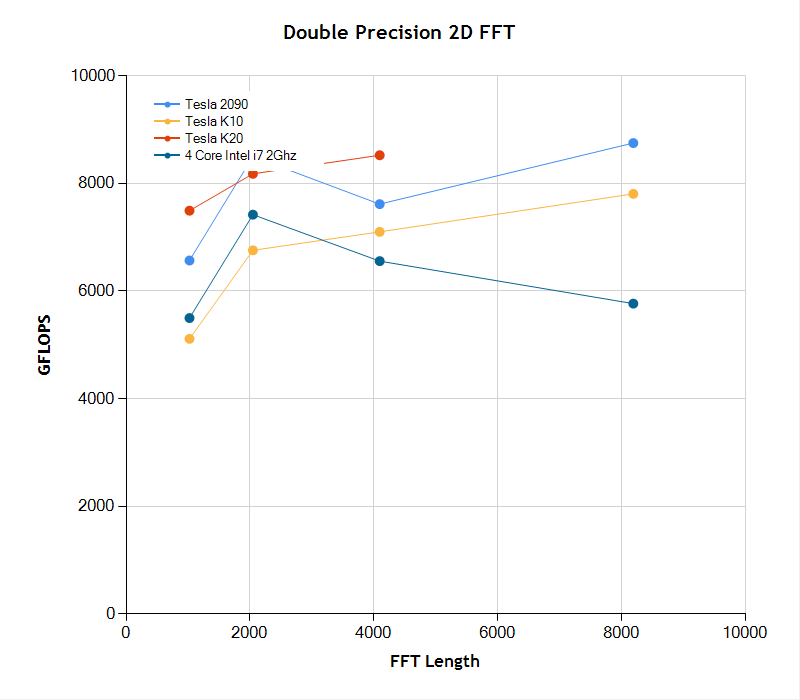
The 2D FFT case is different because of the higher computational demand of the two-dimensional case. First, in the single precision case we see the inferiority of the NVIDIA K20, which is designed primarily as a double precision computation engine. Here the CPU-bound outperforms the K20 for all image sizes. However the K10 and 2090 are extremely fast (including the data transfer time) and outperform the CPU-bound 2D FFT by approximately 60-70%. In the double precision 2D FFT case, the K20 outperforms all other processors in nearly all cases measured. The tested K20 was memory limited in the [ 8192 x 8192 ] test case and couldn’t complete the computation.
 |
 |
 |
 |
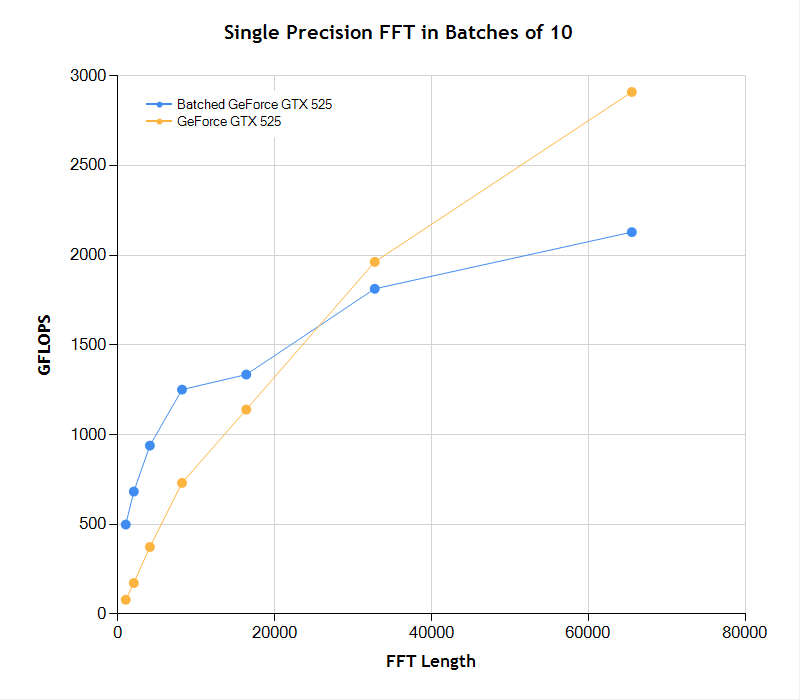
Batch FFT
To amortized the cost of data transfer to and from the GPU, NMath Premium can run FFT’s in batches of signal arrays. For the smaller FFT sizes, the batch processing nearly doubles the performance of the FFT on the GPU. As the length of the FFT increases the advantage of batch processing decreased because the full array signals can no longer be loaded into the GPU.
Summary
As the complexity of the FFT increases either due to an increase in length or problem dimension the GPU leveraged FFT performance overtakes the CPU-bound version. The advantage of the GPU 1D FFT grows substantially as the FFT length grows beyond ~100,000 samples. Batch processing of signals arranged in rows in a matrix can be used to mitigate the data transfer overhead to the GPU. There are times where it may be advantageous to offload the processing of FFT’s onto the GPU even when CPU-bound performance is greater because this will free many CPU cycles for other activities. Because NMath Premium supports adjustable crossover thresholds the developer can control the FFT length at which FFT computation switchs to the GPU. Setting this threshhold to zero will push all FFT processing to the GPU, completely offloading this work from the CPU.