19.3 Sparse Matrix Factorizations (.NET, C#, CSharp, VB, Visual Basic, F#)
NMath
provides classes for computing and storing factorizations of general
sparse matrices. Instances of the factorization
classes calculate solutions to the equation 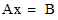 where A is a sparse matrix and B
is a single vector, or multiple vectors.
where A is a sparse matrix and B
is a single vector, or multiple vectors.
Once a factorization is constructed, it can be reused to solve for different right-hand sides.
The factorization classes associated with each general sparse matrix type are shown in Table 16.
Matrix Classes |
Factorization Classes |
Note that there are two factorization classes for symmetric and Hermitian types: one for indefinite matrices, and one for positive definite (PD) matrices.
SparseMatrixFact is the base class for sparse matrix factorizations, and is parameterized on the type, T, of values stored in the vector.
You can create an instance of a factorization class by supplying the constructor with a matrix to factor. The following code creates a symmetric sparse matrix from the given data, then factors the matrix:
Code Example – C# sparse matrix factorization
var sA = new DoubleSymCsrSparseMatrix( sparseData);
var fact = new DoubleSparseSymFact( sA );
Code Example – VB sparse matrix factorization
Dim SA As New DoubleSymCsrSparseMatrix(SparseData)
Dim Fact As New DoubleSparseSymFact(SA)
You can also use an existing instance to factor other matrices with the provided Factor() method. Thus, if sB is another DoubleSymCsrSparseMatrix:
Code Example – C# sparse matrix factorization
fact.Factor( sB );
Code Example – VB sparse matrix factorization
Fact.Factor(SB)
The read-only ErrorStatus property gets an Error enumerated value. For example:
Code Example – C# sparse matrix factorization
if ( fact.ErrorStatus == DoubleSparseSymFact.Error.NoError )
{
// Do something here...
}
Code Example – VB sparse matrix factorization
If Fact.ErrorStatus = DoubleSparseSymFact.Error.NoError Then
' Do something here...
End If
Once a factorization is constructed from a matrix, it can be used to solve for different right hand sides. For instance, this code solves for one right-hand side:
Code Example – C# sparse matrix factorization
var b = new DoubleVector( 8, 1 );
DoubleVector x = fact.Solve( b );
Code Example – VB sparse matrix factorization
Dim B As New DoubleVector(8, 1)
Dim X As DoubleVector = Fact.Solve(B)
Similarly, you can use the Solve() method to solve for multiple right-hand sides. This code solves for 3 right-hand sides:
Code Example – C# sparse matrix factorization
int nrhs = 3;
var B = new DoubleMatrix( 8, nrhs, new RandGenBeta() );
DoubleMatrix X = fact.Solve( B );
Code Example – sparse matrix factorization
Dim NRHS As Integer = 3
Dim B As New DoubleMatrix(8, NRHS, New RandGenBeta())
Dim X As DoubleMatrix = Fact.Solve(B)
The right-hand sides are the columns of matrix B, and the corresponding solutions are the columns of matrix X.
NOTE—Be sure to check the ErrorStatus property on the factorization before calling Solve() to confirm that the factorization is valid.
