19.2 Sparse Matrices (.NET, C#, CSharp, VB, Visual Basic, F#)
NMath provides the classes shown in Table 15 for storing general sparse matrices.
Class |
Description |
Store a general sparse matrix of float or double values. |
|
Extend basic CSR sparse matrix class for matrices symmetric about the diagonal. |
|
Store a general sparse matrix of FloatComplex or DoubleComplex values. |
|
Extend basic complex CSR spare
matrix class for matrices which satisfy |
Only the non-zero elements are stored.
Class SparseMatrixData stores general sparse matrix data, and is parameterized on both the storage format used, and the type, T, of values stored in the vector. Storage formats implement the ISparseMatrixStorage interface. NMath currently provides only one implementation—class CompressedSparseRow, which stores sparse matrix data in compressed row format.
The compressed row storage format (CSR) makes no assumptions about the sparsity structure of the matrix. CSR puts data into three arrays:
● an array of type T values containing the non-zero values of the matrix. The values are mapped into this array in row-major format.
● an integer column index array, where element i is the number of the column that contains the ith element of the values array.
● an integer row index array, where element j gives the index of the element in the values array that is the first non-zero element in the row j. As the row index array gives the location of the first non-zero element within a row, and the non-zero elements are stored consecutively, the number of non-zero elements in the ith row is equal to the difference of rowIndex[i] and rowIndex[i+1]. To have this relationship hold for the last row of the matrix, an additional entry is added to the end of rowIndex. Its value is equal to the number of non-zero elements. This makes the rowIndex array one larger that the number of rows in the matrix.
NOTE—Indexing starts at 0. Each row in compressed sparse row format must contain at least one nonzero entry.
For example, the matrix
| 1 -1 0 -3 0 |
| -2 5 0 0 0 |
A = | 0 0 4 6 4 |
| -4 0 2 7 0 |
| 0 8 0 0 -5 |
is stored as
values = (1, -1, -3, -2, 5, 4, 6, 4, -4, 2, 7, 8, -5)
columns = ( 0, 1, 3, 0, 1, 2, 3, 4, 0, 2, 3, 1, 4 )
rowIndex = ( 0, 3, 5, 8, 11, 13 )
Instances of sparse matrix classes are created in a variety ways. They can be constructed from CompressedSparseRow objects containing the sparse data, like so:
Code Example – C# sparse matrix
var values = new double[4] { 1, 2, 3, 4 };
int[] columns = new int[4] { 0, 2, 1, 0 };
int[] rowIndex = new int[4] { 0, 2, 3, 4 };
int cols = 3;
var sparseData = new CompressedSparseRow<double>( values, columns,
rowIndex, cols );
var sA = new DoubleCsrSparseMatrix( sparseData );
Code Example – VB sparse matrix
Dim Values = New Double() {1.0, 2.0, 3.0, 4.0}
Dim Columns = New Integer() {0, 2, 1, 0}
Dim RowIndex = New Integer() {0, 2, 3, 4}
Dim Cols As Integer = 3
Dim SparseData As New CompressedSparseRow(Of Double)(Values,
Columns, RowIndex, Cols)
Dim SA As New DoubleCsrSparseMatrix(SparseData)
Or they can be constructed from values stored as an IDictionary, where row-column pair are the keys and the non-zero entries are the values:
Code Example – C# sparse matrix
var values = new Dictionary<IntPair, double>();
values.Add( new IntPair( 0, 0 ), 1 );
values.Add( new IntPair( 0, 2 ), 2 );
values.Add( new IntPair( 1, 2 ), 3 );
values.Add( new IntPair( 2, 1 ), 4 );
int cols = 3;
var sA = new DoubleCsrSparseMatrix( values, cols );
Code Example – VB sparse matrix
Dim Values As New Dictionary(Of IntPair, Double)()
Values.Add(New IntPair(0, 0), 1)
Values.Add(New IntPair(0, 2), 2)
Values.Add(New IntPair(1, 2), 3)
Values.Add(New IntPair(2, 1), 4)
Dim Cols As Integer = 3
Dim SA As New DoubleCsrSparseMatrix(Values, Cols)
As a convenience, class SparseMatrixBuilder implements the interface System.Collections.Generic.IDictionary{IntPair,T}, providing matrix-like row and column indexing for setting and retrieving values.
Code Example – C# sparse matrix
var smb = new SparseMatrixBuilder<double>();
smb[0,0] = 1;
smb[0,2] = 2;
smb[1,2] = 3;
smb[2,1] = 4;
int cols = 3;
var sA = new DoubleCsrSparseMatrix( smb, cols );
Code Example – VB sparse matrix
Dim SMB As New SparseMatrixBuilder(Of Double)()
SMB(0, 0) = 1
SMB(0, 2) = 2
SMB(1, 2) = 3
SMB(2, 1) = 4
Dim Cols = 3
Dim SA As New DoubleCsrSparseMatrix(SMB, Cols)
Lastly, sparse matrix can be generated from values in a dense matrix. This code uses the MatrixFunctions.ToSparseMatrix() method to create a DoubleCsrSparseMatrix from the non-zero elements in a DoubleMatrix A:
Code Example – C# sparse matrix
int maxNonzero = 500;
DoubleCsrSparseMatrix sA =
MatrixFunctions.ToSparseMatrix( A, maxNonzero );
Code Example – VB sparse matrix
Dim MaxNonZero As Integer = 500
Dim SA As DoubleCsrSparseMatrix =
MatrixFunctions.ToSparseMatrix(A, MaxNonZero)
Accessing and Modifying Sparse Matrix Values
Sparse matrix classes inherit the following properties from SparseMatrixData:
● Rows gets the number of rows in the matrix.
● Cols gets the number of columns in the matrix.
● Data gets and sets the formatted data for the matrix as an ISparseMatrixStorage object.
The sparse matrix classes also provide standard indexers for getting and setting individual element values:
Code Example – C# sparse matrix
double x = sA[4, 100];
Code Example – VB sparse matrix
Dim X As Double = SA(4, 100)
NOTE—Attempts to set zero elements raise a NonModifiableElementException.
Operator == tests for equality of two sparse matrices, and returns true if both vecrtors have the same nonzero elements; otherwise, false. Following the convention of the .NET Framework, if both objects are null, they test equal. Operator != returns the logical negation of ==. The Equals() member function also tests for equality.
NMath provides overloaded arithmetic operators for general sparse matrices with their conventional meanings for those .NET languages that support them, and equivalent named methods for those that do not. All binary operators and equivalent named methods work either with two matrices, or with a matrix and a scalar.
Code Example – C# sparse matrix
double a = 3.18;
var sA1 = new DoubleCsrSparseMatrix( data );
DoubleCsrSparseMatrix sA2 = a * sA1;
Code Example – VB sparse matrix
Dim A As Double = 3.18
Dim SA1 As New DoubleCsrSparseMatrix(Data)
Dim SA2 As DoubleCsrSparseMatrix = A * SA1
The sparse matrix classes provide the Scale() function to scale each element in a sparse matrix by the specified value. MatrixFunctions also provides a variety of functions that take general sparse matrices as arguments:
● Product() computes the inner product of two sparse matrices, and returns the result as a sparse matrix.
● DenseProduct() computes the inner product of two sparse matrices, and returns the result as a dense matrix.
● TransposeProduct() computes the transpose inner product of two sparse matrices, and returns the result as a sparse matrix.
● DenseTransposeProduct() computes the transpose inner product of two sparse matrices, and returns the result as a dense matrix.
For instance, if sA and sB are DoubleCsrSparseMatrix objects:
Code Example – C# sparse matrix
DoubleCsrSparseMatrix sC = MatrixFunctions.Product( sA, sB )
Code Example – VB sparse matrix
Dim SC As DoubleCsrSparseMatrix = MatrixFunctions.Product(SA, SB)
Creating Dense Matrices from Sparse Matrices
The MatrixFunctions.ToDenseMatrix() method copies the elements of a compressed sparse matrix to a full storage matrix. For example, this code creates a new dense matrix from DoubleCsrSparseMatrix sA:
Code Example – C# sparse matrix
DoubleMatrix A = MatrixFunctions.ToDenseMatrix( sA );
Code Example – VB sparse matrix
Dim A As DoubleMatrix = MatrixFunctions.ToDenseMatrix(SA)

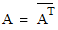 , where
, where 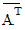 denotes the conjugate
transpose of
denotes the conjugate
transpose of 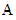 .
.