30.4 Constrained Least Squares (.NET, C#, CSharp, VB, Visual Basic, F#)
When least squares problems are unconstrained, they can be solved by geometric means, such as orthogonal projection. When constraints are introduced, however, nonlinear optimization techniques are required. In NMath, class ConstrainedLeastSquaresProblem encapsulates a constrained least squares problem, which can be solved using class ConstrainedLeastSquares. The problem is solved by reformulating as a quadratic programming problem (Section 30.3).
A least squares problem solves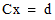 
by minimizing 
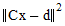. Class ConstrainedLeastSquaresProblem encapsulates
a constrained least squares problem. First construct the problem object
from the matrix C and the vector d.
Code Example – C# constrained least squares
var C = new DoubleMatrix(
"5x4 [0.9501 0.7620 0.6153 0.4057 " +
"0.2311 0.4564 0.7919 0.9354 " +
"0.6068 0.0185 0.9218 0.9169 " +
"0.4859 0.8214 0.7382 0.4102 " +
"0.8912 0.4447 0.1762 0.8936]" );
var d = new DoubleVector( 0.0578, 0.3528, 0.8131, 0.0098, 0.1388 );
var problem = new ConstrainedLeastSquaresProblem( C, d );
Code Example – VB constrained least squares
Dim C As New DoubleMatrix(
"5x4 [0.9501 0.7620 0.6153 0.4057 " &
"0.2311 0.4564 0.7919 0.9354 " &
"0.6068 0.0185 0.9218 0.9169 " &
"0.4859 0.8214 0.7382 0.4102 " &
"0.8912 0.4447 0.1762 0.8936]")
Dim D As New DoubleVector(0.0578, 0.3528, 0.8131, 0.0098, 0.1388)
Dim Problem As New ConstrainedLeastSquaresProblem(C, D)
Next, add the bounds and constraints. Constraints are specified using a constraint matrix, a vector of right-hand sides, and a tolerance. For example, this code adds the inequality constraints Ax <= b using a constraint tolerance of 0.00001. This allows for small violations of the constraints. Specifically the constraints will be considered satisfied for a vector x if Ax <= b + 0.00001.
Code Example – C# constrained least squares
var A = new DoubleMatrix(
"3x4[0.2027 0.2721 0.7467 0.4659 " +
"0.1987 0.1988 0.4450 0.4186 " +
"0.6037 0.0152 0.9318 0.8462]" );
var b = new DoubleVector( 0.5251, 0.2026, 0.6721 );
double constraintTolerance = 0.00001;
for ( int i = 0; i < A.Rows; i++ )
{
problem.AddUpperBoundConstraint( A.Row( i ), b[i],
constraintTolerance );
}
Code Example – VB constrained least squares
Dim A As New DoubleMatrix(
"3x4[0.2027 0.2721 0.7467 0.4659 " &
"0.1987 0.1988 0.4450 0.4186 " &
"0.6037 0.0152 0.9318 0.8462]")
Dim B As New DoubleVector(0.5251, 0.2026, 0.6721)
Dim ConstraintTolerance As Double = 0.00001
Dim I As Integer
For I = 0 To A.Rows - 1
Problem.AddUpperBoundConstraint(A.Row(I), B(I), ConstraintTolerance)
Next
This code add variable bounds -0.1 <= x[i] <= 2.0.
Code Example – C# constrained least squares
for ( int i = 0; i < problem.NumVariables; i++ )
{
problem.AddBounds( i, -0.10, 2.0, .00001 );
}
Code Example – VB constrained least squares
For I = 0 To Problem.NumVariables - 1
Problem.AddBounds(I, -0.1, 2.0, 0.00001)
Next
ConstrainedLeastSquares uses a Quadratic Programming (QP) solver to solve the constrained least squares problem.
Code Example – C# constrained least squares
var solver = new ConstrainedLeastSquares();
bool success = solver.Solve( problem );
Console.WriteLine( "Success = {0}", success );
Console.WriteLine( "Solution x = {0}", solver.X );
Console.WriteLine( "Residual norm = {0}", solver.ResidualNorm );
Console.WriteLine( "Performed {0} iterations", solver.Iterations );
Code Example – VB constrained least squares
Dim Solver As New ConstrainedLeastSquares()
Dim Success As Boolean = Solver.Solve(Problem)
Console.WriteLine("Success = {0}", Success)
Console.WriteLine("Solution x = {0}", Solver.X)
Console.WriteLine("Residual norm = {0}", Solver.ResidualNorm)
Console.WriteLine("Performed {0} iterations", Solver.Iterations)
By default, the QP solver used is the active set solver with default options (Section 30.3). You can also pass in an instance of a QP solver for the constrained least squares class to use. This allows you to set options on the QP solver and inspect results.
Code Example – C# constrained least squares
var interiorPointQp = new InteriorPointQPSolver();
var solverParams = new InteriorPointQPSolverParams
{
MaxIterations = 10000,
PresolveLevel =
InteriorPointQPSolverParams.PresolveLevelOption.None
};
solver.Solve( problem, interiorPointQp,
solverParams );
Console.WriteLine( "Interior point QP result = {0}",
interiorPointQp.Result );
Code Example – VB constrained least squares
Dim InteriorPointQp As New InteriorPointQPSolver()
Dim SolverParams = New InteriorPointQPSolverParams()
SolverParams.MaxIterations = 10000
SolverParams.PresolveLevel =
InteriorPointQPSolverParams.PresolveLevelOption.None
Solver.Solve(Problem, InteriorPointQp, SolverParams)
Console.WriteLine("Interior point QP result = {0}",
InteriorPointQp.Result)
If you use the active set QP solver you can determine which constraints are active in the solution by accessing the Lagrange multiplier property. A constraint is active if its corresponding Lagrange multiplier is nonzero.
Code Example – C# constrained least squares
var activeSetQP = new ActiveSetQPSolver();
solver.Solve( problem, activeSetQP );
// Print out the active constraints.
for ( int i = 0; i < activeSetQP.LagrangeMultiplier.Length; i++ )
{
if ( activeSetQP.LagrangeMultiplier[i] != 0.0 )
{
Console.WriteLine( "Constraint {0} = {1} is active", i,
problem.Constraints[i].ToString() );
}
}
Code Example – VB constrained least squares
Dim ActiveSetQP As New ActiveSetQPSolver()
Solver.Solve(Problem, ActiveSetQP)
'' Print out the active constraints.
For I = 0 To ActiveSetQP.LagrangeMultiplier.Length - 1
If (ActiveSetQP.LagrangeMultiplier(I) <> 0.0) Then
Console.WriteLine("Constraint {0} = {1} is active", I,
Problem.Constraints(I).ToString())
End If
Next