30.3 Quadratic Programming (.NET, C#, CSharp, VB, Visual Basic, F#)
A quadratic programming (QP) problem is a NLP problem with a specific form for the objective and constraint functions. A QP problem has the following form:
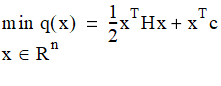
subject to
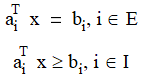
where H is a symmetric nxn matrix, E and I are finite sets of indices, and c, x, and ai are vectors in Rn. The matrix H is the Hessian of the objective function q(x).
NOTE—Only convex QP problems are supported. A QP problem is convex if the matrix H in the objective function is positive definite.
In NMath, class QuadraticProgrammingProblem class encapsulates a QP problem. The objective function is specified by providing the matrix H and the vector c. The matrix H, usually referred to as the Hessian, is the quadratic coefficient matrix. The vector c, sometimes referred to as the gradient, contains the coefficients for the linear terms.
For example, to minimize
q(x) = (x0 - 1)^2 + (x1 - 2.5)^2
Translate the objective function into the form 0.5*x'Hx + x'c. In this case:
H = | 2 0 |
| 0 2 |
c = [-2 -5]
This code sets up the QP problem:
Code Example – C# quadratic programming problem
var H = new DoubleMatrix( "2x2[2 0 0 2]" );
var c = new DoubleVector( -2.0, -5.0 );
var problem = new QuadraticProgrammingProblem( H, c );
Code Example – VB quadratic programming problem
Dim H As New DoubleMatrix("2x2[2 0 0 2]")
Dim C As New DoubleVector(-2.0, -5.0)
Dim Problem As New QuadraticProgrammingProblem(H, C)
The constraints in a QP problem must be linear. There are several convenience methods provided for adding constraints and variable bounds.
For instance, given constraints:
-x0 + 2*x1 <= 2
x0 - 2*x1 >= -6
-x0 + 2*x1 >= -2
x0 >= 0
x1 >= 0
The following code adds these constraints to an existing QuadraticProgrammingProblem object:
Code Example – C# quadratic programming problem
problem.AddUpperBoundConstraint(
new DoubleVector( -1.0, 2.0 ), 2.0 );
problem.AddLowerBoundConstraint(
new DoubleVector( 1.0, -2.0 ), -6.0 );
problem.AddLowerBoundConstraint(
new DoubleVector( -1.0, 2.0 ), -2.0 );
problem.AddLowerBound( 0, 0 );
problem.AddLowerBound( 1, 0 );
Code Example – VB quadratic programming problem
Problem.AddUpperBoundConstraint( New DoubleVector(-1.0, 2.0), 2.0)
Problem.AddLowerBoundConstraint( New DoubleVector(1.0, -2.0), -6.0)
Problem.AddLowerBoundConstraint( New DoubleVector(-1.0, 2.0), -2.0)
Problem.AddLowerBound(0, 0)
Problem.AddLowerBound(1, 0)
NMath provides two classes for solving quadratic programming problems:
● Class ActiveSetQPSolver solves QP problems using an active set algorithm.
● Class InteriorPointQPSolver solves QP problems using an interior point algorithm.
Active Set
Class ActiveSetQPSolver solves QP problems using an active set algorithm. The active set contains a subset of inequalities to watch while searching for a solution, which reduces the complexity of the search.
Code Example – C# active set quadratic programming
var solver = new ActiveSetQPSolver();
Code Example – VB active set quadratic programming
Dim Solver As New ActiveSetQPSolver()
The Solve() method solves the problem, and returns true if the algorithm terminated successfully:
Code Example – C# active set quadratic programming
if ( !solver.Solve( problem ) ) {
Console.WriteLine( "Solver failed: {0}", solver.Status );
}
else {
Console.WriteLine("Solver found solution (x0, x1) = ({0}, {1})",
solver.OptimalX[0], solver.OptimalX[1] );
Console.WriteLine("After {0} iterations", solver.Iterations );
Console.WriteLine( "Optimal objective function value = {0}",
solver.OptimalObjectiveFunctionValue );
}
Code Example – VB active set quadratic programming
If Not Solver.Solve(Problem) Then
Console.WriteLine("Solver failed: {0}", Solver.Status)
Else
Console.WriteLine("Solver found solution (x0, x1) = ({0}, {1})",
Solver.OptimalX(0), Solver.OptimalX(1))
Console.WriteLine("After {0} iterations", Solver.Iterations)
Console.WriteLine("Optimal objective function value = {0}",
Solver.OptimalObjectiveFunctionValue)
End If
The Solve() method also optionally accepts a starting point for the solution search. The starting point need not be a feasible point.
Interior Point
Class InteriorPointQPSolver solves QP problems using an interior point algorithm.
Code Example – C# interior point quadratic programming
var solver = new InteriorPointQPSolver();
Code Example – VB interior point quadratic programming
Dim Solver As New InteriorPointQPSolver()
Parameters are specified using an instance of InteriorPointQPSolverParams.
Code Example – C# interior point quadratic programming
var solverParams = new InteriorPointQPSolverParams
{
KktForm = InteriorPointQPSolverParams.KktFormOption.Blended,
Tolerance = 1e-6,
MaxDenseColumnRatio = 0.9,
PresolveLevel =
InteriorPointQPSolverParams.PresolveLevelOption.Full,
SymbolicOrdering = InteriorPointQPSolverParams.
SymbolicOrderingOption.ApproximateMinDegree
};
Code Example – VB interior point quadratic programming
Dim SolverParams As New InteriorPointQPSolverParams
SolverParams.KktForm =
InteriorPointQPSolverParams.KktFormOption.Blended
SolverParams.Tolerance = "1e-6"
SolverParams.MaxDenseColumnRatio = 0.9
SolverParams.PresolveLevel =
InteriorPointQPSolverParams.PresolveLevelOption.Full
SolverParams.SymbolicOrdering = InteriorPointQPSolverParams.
SymbolicOrderingOption.ApproximateMinDegree
This code performs the actual solve and prints out the results:
Code Example – C# interior point quadratic programming
solver.Solve( problem, solverParams );
Console.WriteLine( "Solver Parameters:" );
Console.WriteLine( solverParams.ToString() );
Console.WriteLine( "\nResult = " + solver.Result );
Console.WriteLine( "Optimal x = " + solver.OptimalX );
Console.WriteLine( "Optimal Function value = " +
solver.OptimalObjectiveFunctionValue );
Console.WriteLine( "iterations = " + solver.IterationCount );
Code Example – VB interior point quadratic programming
Console.WriteLine("Solver Parameters:")
Console.WriteLine(SolverParams.ToString())
Console.WriteLine()
Console.WriteLine("Result = {0}", Solver.Result)
Console.WriteLine("Optimal x = {0}", Solver.OptimalX)
Console.WriteLine("Optimal Function value = {0}",
Solver.OptimalObjectiveFunctionValue)
Console.WriteLine("iterations = {0}", Solver.IterationCount)
