22.1 QR Decompositions (.NET, C#, CSharp, VB, Visual Basic, F#)
A QR decomposition is a representation of a matrix A of the form:
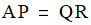
where P is a permutation matrix, Q is orthogonal, and R is upper trapezoidal (or upper triangular if A has more rows than columns and full rank).
NMath provides QR decomposition classes for four datatypes: single- and double-precision floating point numbers, and single- and double-precision complex numbers. The classnames are FloatQRDecomp, DoubleQRDecomp, FloatComplexQRDecomp, and DoubleComplexQRDecomp.
Instances of the QR decomposition classes are constructed from general matrices of the appropriate datatype. For example, this code creates a FloatQRDecomp from a FloatMatrix:
Code Example – C# QR decomposition
var A =
new FloatMatrix( "5x3 [ 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 ]" );
var qr = new FloatQRDecomp( A );
Code Example – VB QR decomposition
Dim A As New FloatMatrix(
"5x3 [ 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 ]")
Dim QR As New FloatQRDecomp(A)
By default, pivoting is done so that the entries along the diagonal of R are non-increasing. For greater control, NMath provides QR decomposition server classes that create QR decomposition objects with non-default decomposition parameters. The classnames are FloatQRDecompServer, DoubleQRDecompServer, FloatComplexQRDecompServer, and DoubleComplexQRDecompServer.
The QR decomposition server classes all have the same interface:
● The Pivoting property sets whether or not pivoting is performed. By default, pivoting is true.
● The SetInitialColumn() method moves a given column to the beginning of AP before the computation, and fixes it in place during the computation.
● The SetFreeColumn() method allows a given column to be interchanged during the computation with any other free column. By default, all columns are free.
● The GetDecomp() method takes a matrix and returns a decomposition object using the current pivoting parameters.
For example, this code uses a DoubleComplexQRDecompServer to turn off pivoting:
Code Example – C# QR decomposition
var qrs = new DoubleComplexQRDecompServer();
qrs.Pivoting = false;
int rows = 10, cols = 3;
var A = new DoubleComplexMatrix( rows, cols,
new RandGenUniform( -1, 1 ) );
DoubleComplexQRDecomp qr = qrs.GetDecomp( A );
Code Example – VB QR decomposition
Dim QRS As New DoubleComplexQRDecompServer()
QRS.Pivoting = False
Dim Rows As Integer = 10
Dim Cols As Integer = 3
Dim A As New DoubleComplexMatrix(Rows, Cols,
New RandGenUniform(-1.0, 1.0))
Dim QR As DoubleComplexQRDecomp = QRS.GetDecomp(A)
This code moves column 7 to the beginning of AP before the computation, and fixes it in place during the computation:
Code Example – C# QR decomposition
var qrs = new DoubleQRDecompServer();
qrs.SetIntialColumn( 7 );
int rows = 20, cols = 12;
var A = new DoubleMatrix( rows, cols,
new RandGenUniform(-1,1) );
DoubleQRDecomp qr = qrs.GetDecomp( A );
Code Example – VB QR decomposition
Dim QRS As New DoubleQRDecompServer()
QRS.SetIntialColumn(7)
Dim Rows As Integer = 20
Dim Cols As Integer = 12
Dim A As New DoubleMatrix(Rows, Cols,
New RandGenUniform(-1.0, 1.0))
Dim QR As DoubleQRDecomp = QRS.GetDecomp(A)
Once a QR decomposition object has been constructed from a matrix, various read-only properties are provided for retrieving the elements of the decomposition, and for retrieving information about the original matrix:
● P gets the permutation matrix.
● Q gets the orthogonal matrix.
● R gets the upper trapezoidal matrix.
● Rows gets the number of rows in the original matrix A.
● Cols gets the number of columns in the original matrix A.
For example:
Code Example – C# QR decomposition
int rows = 10, cols = 3;
DoubleMatrix A =
new DoubleMatrix( rows, cols, new RanGenUniform( 1, -1 ) );
var qr = new DoubleQRDecomp( A );
DoubleMatrix Q = qr.Q;
DoubleMatrix R = qr.R;
DoubleMatrix P = qr.P;
Code Example – VB QR decomposition
Dim Rows As Integer = 10
Dim Cols As Integer = 3
Dim A As New DoubleMatrix(Rows, Cols,
New RandGenUniform(-1.0, 1.0))
Dim QR As New DoubleQRDecomp(A)
Dim Q As DoubleMatrix = QR.Q
Dim R As DoubleMatrix = QR.R
Dim P As DoubleMatrix = QR.P
Methods are also provided for manipulating the component matrices P, Q, or R:
● Px(), Qx(), and Rx() compute the inner product of a component matrix and a given vector.
● PTx(), QTx(), and RTx() compute the inner product of the transpose of a component matrix and a given vector, or conjugate transpose for complex types.
● QM() computes the inner product of the orthogonal matrix Q and a given matrix. QTM() uses the transpose of Q, or conjugate transpose for complex types.
● RInvx() computes the inner product of the inverse of the the upper trapezoidal matrix R and a given vector. RTInvx() uses the transpose of R, or conjugate transpose for complex types.
● RDiagonal() returns the main diagonal of the upper trapezoidal matrix R.
These methods are more efficient than retrieving a component matrix using the P, Q, and R properties and manipulating it yourself.
For example:
Code Example – C# QR decomposition
int rows = 12, cols = 20;
var A = new FloatComplexMatrix( rows, cols, rng );
var qr = new FloatComplexQRDecomp( A );
var x = new FloatComplexVector( qr.P.Cols, 1, 1 );
FloatComplexVector y = qr.Px( x );
Code Example – VB QR decomposition
Dim Rows As Integer = 12
Dim Cols As Integer = 20
Dim A As New FloatComplexMatrix(Rows, Cols, rng)
Dim QR As New FloatComplexQRDecomp(A)
Dim X As New FloatComplexVector(QR.P.Cols, 1, 1)
Dim Y As FloatComplexVector = QR.Px(X)
An existing decomposition object can be reused with another matrix using the Factor() method:
Code Example – C# QR decomposition
int rows = 10, cols = 3;
var rng = new RandGenUniform( -1, 1 );
var A = new FloatMatrix( rows, cols, rng );
var qr = new FloatQRDecomp( A );
FloatMatrix Q1 = qr.Q;
FloatMatrix R1 = qr.R;
FloatMatrix P1 = qr.P;
rows = 7;
cols = 7;
var B = new FloatMatrix( rows, cols, rng );
qr.Factor( B );
FloatMatrix Q2 = qr.Q;
FloatMatrix R2 = qr.R;
FloatMatrix P2 = qr.P;
Code Example – VB QR decomposition
Dim Rows As Integer = 10
Dim Cols As Integer = 3
Dim RNG As New RandGenUniform(-1.0, 1.0)
Dim A As New FloatMatrix(Rows, Cols, RNG)
Dim QR As New FloatQRDecomp(A)
Dim Q1 As FloatMatrix = QR.Q
Dim R1 As FloatMatrix = QR.R
Dim P1 As FloatMatrix = QR.P
Rows = 7
Cols = 7
Dim B As New FloatMatrix(Rows, Cols, RNG)
QR.Factor(B)
Dim Q2 As FloatMatrix = QR.Q
Dim R2 As FloatMatrix = QR.R
Dim P2 As FloatMatrix = QR.P
