22.2 Singular Value Decompositions (.NET, C#, CSharp, VB, Visual Basic, F#)
A singular value decomposition (SVD) is a representation of a matrix A of the form:
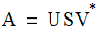
where U and V are orthogonal, S is diagonal, and V* denotes the transpose of a real matrix V or the conjugate transpose of a complex matrix V. The entries along the diagonal of S are the singular values. The columns of U are the left singular vectors, and the columns of V are the right singular vectors.
Creating Singular Value Decompositions
NMath provides singular value decomposition classes for four datatypes: single- and double-precision floating point numbers, and single- and double-precision complex numbers. The classnames are FloatSVDecomp, DoubleSVDecomp, FloatComplexSVDecomp, and DoubleComplexSVDecomp.
Instances of the singular value decomposition classes are constructed from general matrices of the appropriate datatype. For example, this code creates a DoubleSVDecomp from a DoubleMatrix:
Code Example – C# SVD
DoubleMatrix A =
new DoubleMatrix( "4 x 3 [ 1 2 3 12 -2 6 -8 9 11 5 7 -1]" );
var svd = new DoubleSVDecomp( A );
Code Example – VB SVD
Dim A As New DoubleMatrix(
"4 x 3 [ 1 2 3 12 -2 6 -8 9 11 5 7 -1]")
Dim SVD As New DoubleSVDecomp(A)
By default, the reduced singular value decomposition and all singular vectors are computed. For greater control, NMath provides singular value decomposition server classes that create singular value decomposition objects with non-default decomposition parameters. The classnames are FloatSVDecompServer, DoubleSVDecompServer, FloatComplexSVDecompServer, and DoubleComplexSVDecompServer.
The singular value decomposition server classes all have the same interface:
● The ComputeFull property gets and sets whether the full or reduced singular value decomposition is computed. (If matrix A is square, the full and reduced singular value decompositions are the same.)
● The ComputeLeftVectors property gets and sets whether or not the left singular vectors are computed.
● The ComputeRightVectors property gets and sets whether or not the right singular vectors are computed.
● The Tolerance property gets and sets the tolerance for truncating all singular values. Values less than the tolerance are set to zero.
● The GetDecomp() method takes a matrix and returns a singular value decomposition object using the current decomposition parameters.
For example, this code uses a FloatComplexSVDecompServer to turn off the computation of the singular vectors:
Code Example – C# SVD
var svds = new FloatComplexSVDecompServer();
svds.ComputeLeftVectors = false;
svds.ComputeRightVectors = false;
int rows = 10, cols = 10;
var A = new FloatComplexMatrix( rows, cols,
new RandGenUniform( -1, 1 ) );
FloatComplexSVDecomp svd = svds.GetDecomp( A );
Code Example – VB SVD
Dim SVDS As New FloatComplexSVDecompServer()
SVDS.ComputeLeftVectors = False
SVDS.ComputeRightVectors = False
Dim Rows As Integer = 10
Dim Cols As Integer = 10
Dim A As New FloatComplexMatrix(Rows, Cols,
New RandGenUniform(-1.0, 1.0))
Dim SVD As FloatComplexSVDecomp = SVDS.GetDecomp(A)
Using Singular Value Decompositions
Once a singular value decomposition object has been constructed from a matrix, various read-only properties are provided for retrieving the elements of the decomposition, and for retrieving information about the original matrix:
● LeftVectors gets the matrix whose columns are the left singular vectors.
● RightVectors gets the matrix whose columns are the right singular vectors.
● NumberLeftVectors gets the number of left singular vectors.
● NumberRigthVectors gets the number of right singular vectors.
● SingularValues gets the singular values of this decomposition. The values are non-negative and arranged in decreasing order.
● Rank gets the rank of the original matrix A.
● Rows gets the number of rows in the original matrix A.
● Cols gets the number of columns in the original matrix A.
● Fail gets the status of the decomposition. The property returns true if the decomposition algorithm failed to converge; otherwise, false.
For instance:
Code Example – C# SVD
int rows = 5, cols = 5;
var A =
new FloatMatrix( rows, cols, new RandGenUniform( 1, -1 ) );
var svd = new FloatSVDecomp( A );
FloatMatrix U = svd.LeftVectors;
FloatMatrix V = svd.RightVectors;
FloatVector s = svd.SingularValues;
Code Example – VB SVD
Dim Rows As Integer = 5
Dim Cols As Integer = 5
Dim A As New FloatMatrix(rows, cols,
New RandGenUniform(-1.0, 1.0))
Dim SVD As New FloatSVDecomp(A)
Dim U As FloatMatrix = svd.LeftVectors
Dim Y As FloatMatrix = svd.RightVectors
Dim S As FloatVector = svd.SingularValues
Methods are also provided for retrieving individual singular vectors and singular values:
● LeftVector() returns a specified left singular vector.
● RightVector() returns a specified right singular vector.
● SingularValue() returns a specified singular value.
For example, this code returns the first singular value, which is equal to the Euclidean (L2) norm of the matrix A:
Code Example – C# SVD
int rows = 12, cols = 6;
var A = new DoubleComplexMatrix( rows, cols,
new RandGenUniform( -1, 1) );
var svd = new DoubleComplexSVDecomp( A );
double l2 = svd.SingularValue( 0 );
Code Example – VB SVD
Dim Rows As Integer = 12
Dim Cols As Integer = 6
Dim A As New DoubleComplexMatrix(Rows, Cols,
New RandGenUniform(-1.0, 1.0))
Dim SVD As New DoubleComplexSVDecomp(A)
Dim L2 As Double = SVD.SingularValue(0)
Lastly, a Truncate() method is provided that sets all singular values less than a given tolerance to zero. Corresponding singular vectors are also removed.
NOTE—This method can change the numerical rank of the matrix A, which is equal to the number of non-zero singular values.
Code Example – C# SVD
var A = new DoubleMatrix(
"5x5[1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5]" );
var svd = new DoubleSVDecomp( A );
int fullRank = svd.Rank; // == 5
svd.Truncate( 1e-14 );
int deficientRank = svd.Rank; // == 2
Code Example – VB SVD
Dim A As New DoubleMatrix(
"5x5[1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5]")
Dim SVD As New DoubleSVDecomp(A)
Dim FullRank As Integer = SVD.Rank ' == 5
SVD.Truncate("1e-14")
Dim DeficientRanks As Integer = svd.Rank ' == 2
Reusing Singular Value Decompositions
An existing decomposition object can be reused with another matrix using the Factor() method:
Code Example – C# SVD
int rows = 12, cols = 6;
FloatMatrix A =
new FloatMatrix( rows, cols, new RandGenUniform( -1, 1 ) );
var svd = new DoubleSVDecomp( A );
FloatVector svA = svd.SingularValues;
var B = new DoubleMatrix(
"5x5[1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5]" );
svd.Factor( B );
FloatVector svB = svd.SingularValues;
Code Example – VB SVD
Dim Rows As Integer = 12
Dim Cols As Integer = 6
Dim A As New FloatMatrix(Rows, Cols, New RandGenUniform(-1.0, 1.0))
Dim SVD As New DoubleSVDecomp(A)
Dim SVA As FloatVector = SVD.SingularValues
Dim B As New DoubleMatrix(
"5x5[1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5]")
SVD.Factor(B)
Dim SVB As FloatVector = svd.SingularValues
