40.1 Distribution Classes (.NET, C#, CSharp, VB, Visual Basic, F#)
The NMath Stats probability distribution classes are listed in Table 27.
Class |
Distribution |
Beta distribution |
|
Binomial distribution |
|
Chi-Square ( |
|
Exponential distribution |
|
F distribution |
|
Gamma distribution |
|
Geometric distribution |
|
Johnson distribution |
|
Logistic distribution |
|
Log-normal distribution |
|
Negative Binomial distribution |
|
Normal (Gaussian) distribution |
|
Poisson distribution |
|
Student's t distribution |
|
Triangular distribution |
|
Uniform distribution |
|
Weibull distribution |
All distribution classes share a common interface. Class ProbabilityDistribution is the abstract base class for the distribution classes, and provides the following abstract methods implemented by the derived classes:
● PDF() computes the probability density function at a given x.
● CDF() computes the cumulative distribution function at a given x.
● InverseCDF() computes the inverse cumulative distribution function for a given probability p—that is, it returns x such that CDF( x ) = p.
In addition, all NMath Stats distribution classes implement the IRandomVariableMoments interface, which provides the following read-only properties:
● Mean gets the mean of the distribution.
● Variance gets the variance of the distribution.
● Kurtosis gets the kurtosis of the distribution.
● Skewness gets the skewness of the distribution.
Variance is the square of the standard deviation. Kurtosis is a measure of the degree of peakednesss of a distribution; skewness is a measure of the degree of asymmetry.
Once you have constructed a derived distribution type, you can query it for the PDF, CDF, inverse CDF, and random variable moments. For example, this code constructs a NormalDistribution with mean 0 and variance 1, then queries it:
Code Example – C# normal distribution
var dist = new NormalDistribution( 0, 1 );
double pdf = dist.PDF( 0 );
double cdf = dist.CDF( 0 );
double invCdf = dist.InverseCDF( .5 );
double mean = dist.Mean;
double var = dist.Variance;
double kurt = dist.Kurtosis;
double skew = dist.Skewness;
Code Example – VB normal distribution
Dim Dist As New NormalDistribution(0, 1)
Dim PDF As Double = Dist.PDF(0)
Dim CDF As Double = Dist.CDF(0)
Dim InvCDF As Double = Dist.InverseCDF(0.5)
Dim Mean As Double = Dist.Mean
Dim Var As Double = Dist.Variance
Dim Kurt As Double = Dist.Kurtosis
Dim Skew As Double = Dist.Skewness
Class BetaDistribution
represents the beta probability distribution.
The beta distribution is a family of curves with two free parameters,
usually labelled 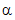 and
and 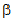 .
Beta distributions are nonzero only on the interval (0
1).
.
Beta distributions are nonzero only on the interval (0
1).
The distribution function for the beta distribution is:
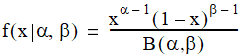
where 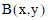 is the beta
function. The beta CDF is the same as the incomplete beta function.
is the beta
function. The beta CDF is the same as the incomplete beta function.
For example, this code constructs a BetaDistribution:
Code Example – C# beta distribution
double alpha = 3;
double beta = 7;
var dist = new BetaDistribution( alpha, beta );
Code Example – VB beta distribution
Dim Alpha As Double = 3
Dim Beta As Double = 7
Dim Dist As New BetaDistribution(Alpha, Beta)
The default constructor creates a BetaDistribution
with 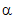 and
and
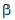 equal
to 1:
equal
to 1:
Code Example – C# beta distribution
var dist = new BetaDistribution();
Code Example – VB beta distribution
Dim Dist As New BetaDistribution()
The provided Alpha and Beta properties can be used to get and set the shape parameters after construction:
Code Example – C# beta distribution
dist.Alpha = 4;
dist.Beta = 10;
Code Example – VB beta distribution
Dist.Alpha = 4
Dist.Beta = 10
Once you have constructed a BetaDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class BinomialDistribution represents the discrete probability distribution of obtaining exactly n successes in N trials where the probability of success on each trial is p. For example, this code constructs an BinomialDistribution:
Code Example – C# binomial distribution
int n = 20;
double p = 0.25;
var bin = new BinomialDistribution( n, p );
Code Example – VB binomial distribution
Dim N As Integer = 20
Dim P As Double = 0.25
Dim Bin As New BinomialDistribution(N, P)
The default constructor creates an BinomialDistribution
with 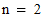 and
and
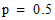 :
:
Code Example – C# binomial distribution
var bin = new BinomialDistribution();
Code Example – VB binomial distribution
Dim Bin As New BinomialDistribution()
The provided N and P properties can be used to get and set the number of trials and the probability of success on each trial after construction:
Code Example – C# binomial distribution
bin.N = 75;
bin.P = 0.02;
Code Example – VB binomial distribution
Bin.N = 75
Bin.P = 0.02
Once you have constructed an BinomialDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class ChiSquareDistribution
represents the chi-square (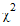 ) probability
distribution. The chi-square distribution is a special case of the gamma
distribution with
) probability
distribution. The chi-square distribution is a special case of the gamma
distribution with 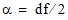 and
and 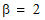 ,
where df is the degrees of freedom.
,
where df is the degrees of freedom.
For example, this code constructs a ChiSquareDistribution:
Code Example – C# chi-square distribution
double df = 16;
var chiSq = new ChiSquareDistribution( df );
Code Example – VB chi-square distribution
Dim DF As Double = 16
Dim ChiSq As New ChiSquareDistribution(DF)
The default constructor creates a ChiSquareDistribution with 1 degree of freedom:
Code Example – C# chi-square distribution
var chiSq = new ChiSquareDistribution();
Code Example – VB chi-square distribution
Dim ChiSq As New ChiSquareDistribution()
The provided DegreesOfFreedom property can be used to get and set the degrees of freedom of the distribution after construction:
Code Example – C# chi-square distribution
chiSq.DegreesOfFreedom = 10;
Code Example – VB chi-square distribution
ChiSq.DegreesOfFreedom = 10
Once you have constructed a ChiSquareDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class ExponentialDistribution represents the exponential distribution. A random variable w is said to have an exponential distribution if it has a probability density function
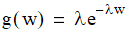
where 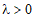 is often called
the rate parameter. The mean of an
exponential distribution is
is often called
the rate parameter. The mean of an
exponential distribution is 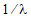 , and the variance
is
, and the variance
is 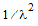 . For
example, this code constructs an ExponentialDistribution:
. For
example, this code constructs an ExponentialDistribution:
Code Example – C# exponential distribution
double lambda = 22;
var exp = new ExponentialDistribution( lambda );
Code Example – VB exponential distribution
Dim Lambda As Double = 22
Dim Exp As New ExponentialDistribution(Lambda)
The provided Lambda property can be used to get and set the rate after construction:
Code Example – C# exponential distribution
exp.Lambda = 15;
Code Example – VB exponential distribution
Exp.Lambda = 15
Once you have constructed an ExponentialDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class FDistribution represents the F probability distribution. The F distribution is the ratio of two chi-square distributions with degrees of freedom df1 and df2, respectively, where each chi-square has first been divided by its degrees of freedom. For example, this code constructs an FDistribution:
Code Example – C# F distribution
double df1 = 11;
double df2 = 19;
var f = new FDistribution( df1, df2 );
Code Example – VB F distribution
Dim DF1 As Double = 11
Dim DF2 As Double = 19
Dim F As New FDistribution(DF1, DF2)
The default constructor creates an FDistribution with both degrees of freedom equal to 1:
Code Example – C# F distribution
var f = new FDistribution();
Code Example – VB F distribution
Dim F As New FDistribution()
The provided DegreesOfFreedom1 and DegreesOfFreedom2 properties can be used to get and set the degrees of freedom after construction:
Code Example – C# F distribution
f.DegreesOfFreedom1 = 15;
f.DegreesOfFreedom2 = 23;
Code Example – VB F distribution
F.DegreesOfFreedom1 = 15
F.DegreesOfFreedom2 = 23
Once you have constructed an FDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class GammaDistribution
represents the gamma probability distribution.
The gamma distribution is a family of curves with two free parameters,
usually labelled 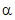 and
and 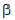 .
The mean of the distribution is
.
The mean of the distribution is 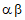 ; the variance
is
; the variance
is 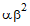 . When
. When
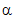 is large,
the gamma distribution closely approximates a normal distribution.
is large,
the gamma distribution closely approximates a normal distribution.
The distribution function for the gamma distribution is:
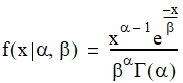
where 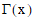 is the Gamma
function.
is the Gamma
function.
For example, this code constructs a GammaDistribution:
Code Example – C# gamma distribution
double alpha = 7;
double beta = 12;
var gamma = new GammaDistribution( alpha, beta );
Code Example – VB gamma distribution
Dim Alpha As Double = 7
Dim Beta As Double = 12
Dim Gamma As New GammaDistribution(Alpha, Beta)
The default constructor creates a GammaDistribution
with 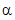 and
and
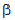 equal
to 1:
equal
to 1:
Code Example – C# gamma distribution
var gamma = new GammaDistribution();
Code Example – VB gamma distribution
Dim Gamma As New GammaDistribution()
The provided Alpha and Beta properties can be used to get and set the shape parameters after construction:
Code Example – C# gamma distribution
gamma.Alpha = 10;
gamma.Beta = 15;
Code Example – VB gamma distribution
Gamma.Alpha = 10
Gamma.Beta = 15
Once you have constructed a GammaDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class GeometricDistribution
represents the geometric distribution. The
geometric distribution is the probability distribution of the number
of failures before the first success. It is supported on the set 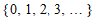 .
.
A GeometricDistribution
is constructed from a given probability of success p,
where 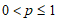 .
For example:
.
For example:
Code Example – C# geometric distribution
double p = .25;
var geo = new GeometricDistribution( p );
Code Example – VB geometric distribution
Dim P As Double = 0.25
Dim Geo As New GeometricDistribution(P)
Class GeometricDistribution provides property P that gets and sets the probability for success for the distribution.
Code Example – C# geometric distribution
geo.P = .5;
Code Example – VB geometric distribution
Geo.P = 0.5
Once you have constructed a GeometricDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class JohnsonDistribution represents the Johnson system of distributions. The Johnson system is based on three possible transformations of a normal random variable—exponential, logistic, and hyperbolic sine—plus the identity transformation:
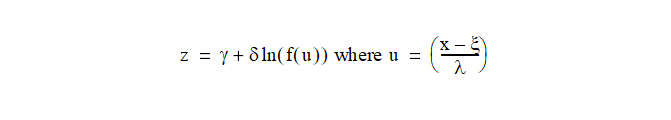
where the transformation f() has four possible forms based on the distribution type:
● Normal (SN): f(u) = exp(u)
● Log Normal (SL): f(u) = u
● Unbounded (SU): f(u) = u + sqrt(1+u^2)
● Bounded (SB): f(u) = u/(1-u)
A JohnsonDistribution instance is constructed from a set of distribution parameter values, and a JohnsonTransformationType enumerated value specifying the transformation type. For instance:
Code Example – C# Johnson distribution
double gamma = -0.18;
double delta = 2.55;
double xi = -0.14;
double lambda = 2.35;
JohnsonTransformationType type = JohnsonTransformationType.Normal;
var dist =
new JohnsonDistribution( gamma, delta, xi, lambda, type );
Code Example – VB Johnson distribution
Dim Gamma As Double = -0.18
Dim Delta As Double = 2.55
Dim Xi As Double = -0.14
Dim Lambda As Double = 2.35
Dim Type As JohnsonTransformationType =
JohnsonTransformationType.Normal
Dim Dist As New JohnsonDistribution(Gamma, Delta, Xi, Lambda, Type)
Once you have constructed a JohnsonDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class JohnsonDistribution also provides a static Fit() method for fitting a Johnson distribution to a data set. Estimation of the Johnson parameters is done from quantiles that correspond to the cumulative probabilities [0.05, 0.206, 0.5, 0.794, 0.95] using the method of Wheeler (1980).1 For example:
Code Example – C# Johnson distribution
var data = new DoubleVector(-0.09736927, 0.21615254,
0.88246516, 0.20559750, -0.61643584, -0.73479925, -0.13180279,
0.31001699, -1.03968035, -0.18430887, 0.96726726, -0.10828009, -
0.69842067, -0.27594517, 1.11464855, 0.55004396, 1.23667580,
0.13909786, 0.41027510, -0.55845691);
var dist = JohnsonDistribution.Fit(data);
Code Example – VB Johnson distribution
Dim Data As New DoubleVector(-0.09736927, 0.21615254,
0.88246516, 0.2055975, -0.61643584, -0.73479925, -0.13180279,
0.31001699, -1.03968035, -0.18430887, 0.96726726, -0.10828009,
-0.69842067, -0.27594517, 1.11464855, 0.55004396, 1.2366758,
0.13909786, 0.4102751, -0.55845691)
Dim Dist As JohnsonDistribution = JohnsonDistribution.Fit(Data)
The Transform() method transforms data using a JohnsonDistribution object.
Class LogisticDistribution represents the logistic probability distribution with a specified location (mean) and scale. The logistic distribution with location m and scale b has distribution function:
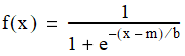
and density:
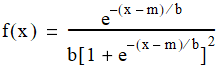
For example, this code constructs a LogisticDistribution:
Code Example – C# logistic distribution
double loc = 2.0;
double scale = 1.5;
var logistic = new LogisticDistribution( loc, scale );
Code Example – VB logistic distribution
Dim Loc As Double = 2.0
Dim Scale As Double = 1.5
Dim Logistic As New LogisticDistribution(Loc, Scale)
The provided Location and Scale properties can be used to get and set distribution parameters after construction:
Code Example – C# logistic distribution
logistic.Location = 7.123;
logistic.Scale = 4.5;
Code Example – VB logistic distribution
Logistic.Location = 7.123
Logistic.Scale = 4.5
Once you have constructed a LogisticDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class LognormalDistribution represents the log-normal distribution. A log-normal distribution has a normal distribution as its logarithm:
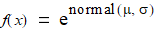
For example, this code constructs an LognormalDistribution whose associated normal distribution has the specified mean and standard deviation:
Code Example – C# log-normal distribution
double mu = -99;
double sigma = 6;
var ln = new LognormalDistribution( mu, sigma );
Code Example – VB log-normal distribution
Dim Mu As Double = -99
Dim Sigma As Double = 6
Dim LN As New LognormalDistribution(Mu, Sigma)
The default constructor creates a LognormalDistribution whose associated normal distribution has mean 0 and standard deviation 1:
Code Example – C# log-normal distribution
var ln = new LognormalDistribution();
Code Example – VB log-normal distribution
Dim LN As New LognormalDistribution()
The Mu and Sigma properties can be used to get and set the mean and standard deviation after construction:
Code Example – C# log-normal distribution
ln.Mu = 2.25;
ln.Sigma = .75;
Code Example – VB log-normal distribution
LN.Mu = 2.25
LN.Sigma = 0.75
Once you have constructed a LognormalDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Negative Binomial Distribution
Class NegativeBinomialDistribution represents the discrete probability distribution of obtaining N successes in a series of x trials, where the probability of success on each trial is P.
For example, this code constructs an NegativeBinomialDistribution:
Code Example – C# negative binomial distribution
int n = 5;
double p = 0.25;
var negBin = new NegativeBinomialDistribution( n, p );
Code Example – VB negative binomial distribution
Dim N As Integer = 5
Dim P As Double = 0.25
Dim NegBin As New NegativeBinomialDistribution(N, P)
The default constructor creates an NegativeBinomialDistribution
with 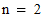 and
and
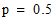 :
:
Code Example – C# negative binomial distribution
var negBin = new NegativeBinomialDistribution();
Code Example – VB negative binomial distribution
Dim NegBin As New NegativeBinomialDistribution()
The provided N and P properties can be used to get and set the number of successes and the probability of success on each trial after construction:
Code Example – C# negative binomial distribution
negBin.N = 75;
negBin.P = 0.02;
Code Example – VB negative binomial distribution
Bin.N = 75
Bin.P = 0.02
Once you have constructed an NegativeBinomialDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class NormalDistribution represents the normal (Gaussian) probability distribution. with a specified mean and variance. For example, this code creates a normal distribution with a mean of 1 and variance of 2.5:
Code Example – C# normal distribution
var norm = new NormalDistribution( 1, 2.5 );
Code Example – VB normal distribution
Dim Norm As New NormalDistribution(1, 2.5)
The default constructor creates a NormalDistribution with mean 0 and variance 1:
Code Example – C# normal distribution
var norm = new NormalDistribution();
Code Example – VB normal distribution
Dim Norm As New NormalDistribution()
The Mean and Variance properties inherited from IRandomVariableMoments can be used to get and set the mean and variance after construction:
Code Example – C# normal distribution
norm.Mean = 2.25;
norm.Variance = .75;
Code Example – VB normal distribution
Norm.Mean = 2.25
Norm.Variance = 0.75
Once you have constructed a NormalDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class PoissonDistribution
represents a poisson distribution with
a specified 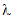 parameter, which is both the mean and the variance of the distribution.
The poisson distribution is the probability of obtaining exactly n successes in N
trials. It is often used as a model for the number of events in a specific
time period. Poisson (1837) showed that the Poisson distribution is the
limiting case of a binomial distribution where N
approaches infinity and p goes to
zero while
parameter, which is both the mean and the variance of the distribution.
The poisson distribution is the probability of obtaining exactly n successes in N
trials. It is often used as a model for the number of events in a specific
time period. Poisson (1837) showed that the Poisson distribution is the
limiting case of a binomial distribution where N
approaches infinity and p goes to
zero while 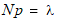 .
The distribution function for the Poisson distribution is:
.
The distribution function for the Poisson distribution is:
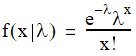
For example, this code constructs a PoissonDistribution:
Code Example – C# poisson distribution
double lambda = 150;
var poisson = new PoissonDistribution( lambda );
Code Example – VB poisson distribution
Dim Lambda As Double = 150
Dim Poisson As New PoissonDistribution(Lambda)
The Mean and Variance properties inherited from IRandomVariableMoments can also be used
to get and set 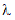 after construction:
after construction:
Code Example – C# poisson distribution
poisson.Mean = 3;
Code Example – VB poisson distribution
Poisson.Mean = 3
Once you have constructed a PoissonDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class TDistribution represents Student's t distribution with specified degrees of freedom. As the number of degrees of freedom grows, the t distribution approaches the normal distribution with mean 0 and variance 1.
For example, this code constructs a TDistribution:
Code Example – C# t distribution
double df = 53;
var t = new TDistribution( df );
Code Example – VB t distribution
Dim DF As Double = 53
Dim T As New TDistribution(DF)
The default constructor creates a TDistribution with 1 degree of freedom:
Code Example – C# t distribution
var t = new TDistribution();
Code Example – VB t distribution
Dim T As New TDistribution()
The provided DegreesOfFreedom property can be used to get and set the degrees of freedom of the distribution after construction:
Code Example – C# t distribution
t.DegreesOfFreedom = 54;
Code Example – VB t distribution
T.DegreesOfFreedom = 54
Once you have constructed a TDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class TriangularDistribution represents the triangular distribution. The triangular distribution is defined by three parameters, a lower limit a, an upper limit b, and number c, between a and b, called the mode. The probability density function has the shape of a triangle in the X/Y plane with vertices (a, 0), (b, 0), and (c, y), where y is chosen so that the area of the triangle is 1.
For example, this code constructs an TriangularDistribution with the given parameters:
Code Example – C# triangular distribution
double lower = 3;
double upper = 10;
double mode = 8;
var td = new TriangularDistribution( lower, upper, mode );
Code Example – VB triangular distribution
Dim Lower As Double = 3
Dim Upper As Double = 10
Dim Mode As Double = 8
Dim TD As New TriangularDistribution(Lower, Upper, Mode)
If you don't specify the mode, the midpoint of the lower and upper limits is used.
The default constructor creates a TriangularDistribution with lower limit 0, upper limit 1, and mode 0.5:
Code Example – C# triangular distribution
var td = new TriangularDistribution();
Code Example – VB triangular distribution
Dim TD As New TriangularDistribution()
The LowerLimit, UpperLimit, and Mode properties can be used to get and set the distribution parameters after construction:
Code Example – C# triangular distribution
td.LowerLimit = 1.5;
td.UpperLimit = 3.5;
td.Mode = 2.75;
Code Example – VB triangular distribution
TD.LowerLimit = 1.5
TD.UpperLimit = 3.5
TD.Mode = 2.75
Once you have constructed a TriangularDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class UniformDistribution represents the uniform distribution. For example, this code constructs an UniformDistribution with the specified lower and upper limits:
Code Example – C# uniform distribution
double lower = -.77;
double upper = 1.22;
var uni = new UniformDistribution( lower, upper );
Code Example – VB uniform distribution
Dim Lower As Double = -0.77
Dim Upper As Double = 1.22
Dim Uni As New UniformDistribution(Lower, Upper)
The default constructor creates a UniformDistribution with lower limit 0 and upper limit 1:
Code Example – C# uniform distribution
var uni = new UniformDistribution();
Code Example – VB uniform distribution
Dim Uni As New UniformDistribution()
The LowerLimit and UpperLimit properties can be used to get and set the lower and upper limits after construction:
Code Example – C# uniform distribution
uni.LowerLimit = 0;
uni.UpperLimit = 2.0;
Code Example – VB uniform distribution
Uni.LowerLimit = 0
Uni.UpperLimit = 2.0
Once you have constructed a UniformDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.
Class WeibullDistribution represents the Weibull distribution. The probability density function of the Weibull distribution is given by:
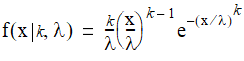
where 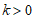 is the shape parameter and
is the shape parameter and 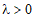 is the scale parameter of the distribution.
is the scale parameter of the distribution.
For example, this code constructs an WeibullDistribution with the specified distribution parameters:
Code Example – C# Weibull distribution
double scale = 1.5;
double shape = 3;
var wb = new WeibullDistribution( scale, shape );
Code Example – VB Weibull distribution
Dim Scale As Double = 1.5
Dim Shape As Double = 3
Dim WB As New WeibullDistribution(Scale, Shape)
The Scale and Shape properties can be used to get and set the distribution parameters after construction:
Code Example – C# Weibull distribution
wb.Scale = .5;
wb.Shape = 2;
Code Example – VB Weibull distribution
WB.Scale = 0.5
WB.Shape = 2
Once you have constructed a WeibullDistribution object, you can query it for the PDF, CDF, inverse CDF, and random variable moments, as described in Section 40.1.

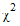 ) distribution
) distribution