17.7 Symmetric Banded Matrices (.NET, C#, CSharp, VB, Visual Basic, F#)
A symmetric banded matrix is a symmetric
matrix (Section 17.3)
that has all its non-zero entries near the diagonal. Entries farther
away from the diagonal than the half bandwidth are defined
to be zero. That is, if 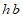 is the half bandwidth, then
is the half bandwidth, then 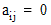 whenever
whenever 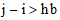 or
or 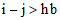 . For example, this is a
5 x 5 symmetric banded matrix with a half bandwidth of 1:
. For example, this is a
5 x 5 symmetric banded matrix with a half bandwidth of 1:
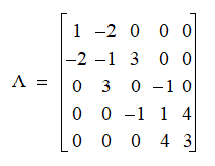
Symmetric banded matrices often arise in one-dimensional finite element problems.
NMath provides symmetric banded matrix classes for single- and double-precision floating point numbers. The classnames are FloatSymBandMatrix and DoubleSymBandMatrix. Hermitian banded matrices are a generalization of symmetric banded matrices for complex types (Section 17.8).
For efficiency, the lower triangular part of the matrix
and zero elements outside the bandwidth are not stored. Instead, matrix
values are stored in a vector column by column. Blank entries are inserted
in the data vector so that the each column takes up the same number of
elements, 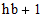 , in the vector.
For example, the following 8 x 8 matrix with a half bandwidth of 2:
, in the vector.
For example, the following 8 x 8 matrix with a half bandwidth of 2:
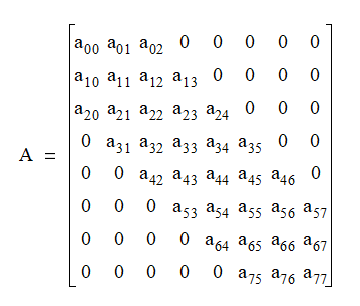
is stored in a data vector as:
v = [x x a00
x a01 a11
a02 a12 a22
a13 a23 a33
a24 a34 a44
a35 a45 a55
a46 a56 a66
a57 a67 a77 ]
where x denotes an unused location.
