17.8 Hermitian Banded Matrices (.NET, C#, CSharp, VB, Visual Basic, F#)
A Hermitian banded matrix is a Hermitian
matrix (Section 17.4)
that has all its non-zero entries near the diagonal. Entries farther
away from the diagonal than the half bandwidth are defined
to be zero. That is, if 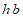 is the half bandwidth, then
is the half bandwidth, then 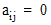 whenever
whenever 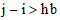 or
or 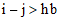 . For example, this is a
5 x 5 Hermitian banded matrix with a half bandwidth of 1:
. For example, this is a
5 x 5 Hermitian banded matrix with a half bandwidth of 1:
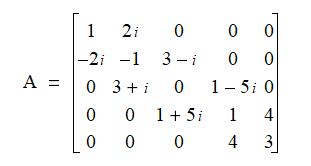
According to the strict definition of a Hermitian matrix,
the diagonal elements must be real numbers, since 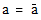 only for real numbers),
while other elements may be complex. NMath
relaxes this requirement and permits complex elements on the diagonal.
The provided MakeDiagonalReal() method sets
the imaginary parts on the main diagonal to zero, thereby meeting the
strict definition of a Hermitian matrix.
only for real numbers),
while other elements may be complex. NMath
relaxes this requirement and permits complex elements on the diagonal.
The provided MakeDiagonalReal() method sets
the imaginary parts on the main diagonal to zero, thereby meeting the
strict definition of a Hermitian matrix.
NMath provides Hermitian banded matrix classes for single- and double-precision complex numbers. The classnames are FloatHermitianBandMatrix and DoubleHermitianBandMatrix. A symmetric banded matrix is a special case of a Hermitian banded matrix where all the elements are real (Section 17.7).
For efficiency, the lower triangular part of the matrix and zero elements outside the bandwidth are not stored. The storage scheme is the same as for a symmetric banded matrix (Section 17.7).
