Chapter 47. Nonnegative Matrix Factorization (.NET, C#, CSharp, VB, Visual Basic, F#)
Nonnegative matrix factorization (NMF) approximately factors a matrix V into two matrices, W and H:
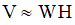
NMF differs from many other factorizations by enforcing the constraint that the factors W and H must be non-negative—that is, all elements must be equal to or greater than zero.
If a set of m n-dimensional data vectors are placed in an n x m matrix V, then NMF can be used to approximately factor V into an n x r matrix W and an r x m matrix H. Usually r is chosen to be much smaller than either m or n, so that W and H are smaller than the original matrix V. Thus, each column v of V is approximated by a linear combination of the columns of W, with the coefficients being the corresponding column h of H, v ≈ Wh. This extracts underlying features of the data as basis vectors in W, which can then be used for identification, classification, and compression. By not allowing negative entries in W and H, NMF enables a non-subtractive combination of the parts to form a whole.
NMath Stats provides classes for basic NMF, and for data clustering using NMF. This chapter describes how to use the NMF classes.
