NMath User's Guide

TOC | Previous | Next | Index

47.1 Nonnegative Matrix Factorization (.NET, C#, CSharp, VB, Visual Basic, F#)

NMath Stats provides class NMFact for performing basic nonnegative matrix factorization (NMF). NMFact uses an iterative algorithm with the goal of minimizing a cost function. The cost function is usually 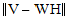, where 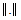denotes the Frobenius matrix norm.

NMFact objects can factor data contained in either a DoubleMatrix or a DataFrame object. The factors W and H are then accessed through properties:

Code Example – C# nonnegative matrix factorization (NMF)

DataFrame data;      // data to be factored

int k;               // number of columns in W

var fact = new NMFact();

fact.Factor( data, k );

Console.WriteLine( "W = " + fact.W );

Console.WriteLine( "H = " + fact.H );

Code Example – VB nonnegative matrix factorization (NMF)

Dim Data As DataFrame '' data to be factored

Dim K As Integer '' number of columns in W

Dim Fact As New NMFact()

Fact.Factor(Data, K)

Console.WriteLine("W = " & Fact.W)

Console.WriteLine("H = " & Fact.H)

Parameters governing aspects of the computation are set through properties or passed as constructor arguments. ComputeCostAtEachStep determines whether or not the cost is computed at each step of the iteration. This can be an expensive calculation and so should generally be done only when you want to investigate convergence properties, such as the convergence rate. If ComputeCostAtEachStep is true, the DoubleVector of costs can be accessed through the StepCost property.

NumIterations specifies the number of iterations performed in the computing of the factorization.

For example:

Code Example – C# nonnegative matrix factorization (NMF)

fact.ComputeCostAtEachStep = true;

fact.NumIterations = numIterations;

Code Example – VB nonnegative matrix factorization (NMF)

Fact.ComputeCostAtEachStep = True

Fact.NumIterations = NumIterations

Update Algorithms

The iterative update step and cost function are specified in a class implementing the INMFUpdateAlgorithm interface. NMath Stats provides four such implementations. All matrices of uniform (0,1) random deviants as the initial values for W and H.

● Class NMFAlsUpdate uses the Alternating Least Squares (ALS) update algorithm. ALS takes advantage of the fact that while the optimization problem is not simultaneously convex in W and H, it is convex in either W or H. Thus, given one matrix, the other can be found with a simple least squares computation:

1. Solve for H in matrix equation W^TWH = W^TV.

2. Set all negative elements of H to 0.

3. Solve for W in the matrix equation HH^TWT = HV^T.

4. Set all negative elements of W to 0.

● Class NMFDivergenceUpdate minimizes a divergence functional. The functional is related to the Poisson likelihood of generating V from W and H:

 

 

 

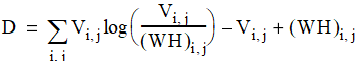
For more information, see Brunet, Jean-Philippe et al., "Metagenes and Molecular Pattern Discovery Using Matrix Factorization", Proceedings of the National Academy of Sciences 101, no. 12 (March 23, 2004): 4164-4169.

● Class NMFGdClsUpdate uses the Gradient Descent - Constrained Least Squares (GDCLS) algorithm. In some cases it may be desirable to enforce a statistical sparsity constraint on the H matrix. As the sparsity of H increases, the basis vectors become more localized—that is, the parts-based representation of the data in W becomes more and more enhanced. The GDCLS algorithm enforces sparsity in H using a scheme that penalizes the number of non-zero entries in H. It is a hybrid algorithm that uses the multiplicative update rule for updating W, while H is calculated using a constrained least squares model as the metric. The algorithm follows:

W_ic ← W_ic((VH^T)_ic / (WHH^T)_ic)

Solve for H in the constrained least squares problem

(W^TW + λI)H = W^TV

Rephrase the constrained least squares step for finding H as

Min_H {||V - WH||² + λ||H||²}

From this it is seen that the parameter λ is a regularization value that is used to balance the reduction of the metric

||V - WH||

with the enforcement of smoothness and sparsity of H.

● Class NMFMultiplicativeUpdate uses a multiplicative update rule for W and H, as proposed by Lee and Seung.

H_cj ← H_cj( (W^TV)_cj / (W^TWH)_cj )

W_ic ← W_ic((VH^T)_ic / (WHH^T)_ic)

This multiplicative method can be classified as a diagonally-scaled gradient descent method.

The update algorithm can be specified either as a constructor argument, or using the UpdateAlgorithm property. For instance:

Code Example – C# nonnegative matrix factorization (NMF)

var alg = new NMFAlsUpdate();

var fact = new NMFact( alg );

fact.Factor( data, k );

Console.WriteLine( "ALS W = " + fact.W );

Console.WriteLine( "ALS H = " + fact.H );

fact.UpdateAlgorithm = new NMFGdClsUpdate();

fact.Factor( data, k );

Console.WriteLine( "GDCLS W = " + fact.W );

Console.WriteLine( "GDCLS H = " + fact.H );

Code Example – VB nonnegative matrix factorization (NMF)

Dim Alg As New NMFAlsUpdate()

Dim Fact As New NMFact(Alg)

Fact.Factor(Data, K)

Console.WriteLine("ALS W = " & Fact.W)

Console.WriteLine("ALS H = " & Fact.H)

Fact.UpdateAlgorithm = New NMFGdClsUpdate()

Fact.Factor(Data, K)

Console.WriteLine("GDCLS W = " & Fact.W )

Console.WriteLine("GDCLS H = " & Fact.H )

Top