32.5 Nonlinear Least Squares Surface Fitting (.NET, C#, CSharp, VB, Visual Basic, F#)
NMath provides classes MultiVariableFunctionFitter and BoundedMultiVariableFunctionFitter for fitting generalized multivariable functions to a set of points. The interface is analogous to OneVariableFunctionFitter and BoundedOneVariableFunctionFitter (Section 32.4), with only a couple changes to accommodate multivariate data. Again, you must supply at least as many data points to fit as your function has parameters.
Generalized Multivariable Functions
A multivariable function takes a vector of x values, and returns a double y:
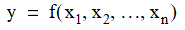
A generalized multivariable function additionally takes a set of parameters, p, which may appear in the function expression in arbitrary ways:
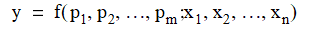
For example, this code computes 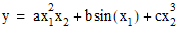 :
:
Code Example – C# nonlinear least squares surface fit
public double MyFunction( DoubleVector p, DoubleVector x )
{
return p[0] * Math.Pow( x[0], 2.0 ) * x[1] +
p[1] * Math.Sin( x[0] ) +
p[2] * Math.Pow( x[1], 3.0 );
};
Code Example – VB nonlinear least squares surface fit
Public Function MyFunction(P As DoubleVector, X As DoubleVector) As
Double
Return P(0) * Math.Pow(X(0), 2.0) * X(1) +
P(1) * Math.Sin(X(0)) +
P(2) * Math.Pow(X(1), 3.0)
End Function
Encapsulating Generalized Multivariable Functions
In NMath, generalized multivariable functions can be encapsulated in two ways:
● By extending the abstract class DoubleParameterizedFunctional, and implementing the Evaluate() method. The GradientWithRespectToParams() can also be implemented to compute the gradient with respect to the parameters; otherwise, a numerical approximation is used.
● By wrapping a Func<DoubleVector, DoubleVector, double> delegate in a DoubleVectorParameterizedDelegate. An Action<DoubleVector, DoubleVector, DoubleVector> delegate can also be provided for computing the gradient with respect to the parameters; otherwise a numerical approximation is used.
For example, this code encapsulates a multivariable function using a DoubleParameterizedFunctional:
Code Example – C# nonlinear least squares surface fit
public class MyFunction : DoubleParameterizedFunctional
{
public MyFunction()
: base (2)
{}
public override double Evaluate( DoubleVector p, DoubleVector x )
{
// z = ayx^2 + bsin(x) + cy^3
return p[0] * x[0] * Math.Pow( x[1], 2.0 ) +
p[1] * Math.Sin( x[0] ) +
p[2] * Math.Pow( x[1], 3.0 );
}
}
DoubleParameterizedFunctional f = new MyFunction();
Code Example – VB nonlinear least squares surface fit
Public Class MyFunction
Inherits DoubleParameterizedFunctional
Sub New()
MyBase.New(2)
End Sub
Public Overrides Function Evaluate(P As DoubleVector, X As
DoubleVector) As Double
' z = ayx^2 + bsin(x) + cy^3
Return P(0) * X(0) * Math.Pow(X(1), 2.0) +
P(1) * Math.Sin(X(0)) +
P(2) * Math.Pow(X(1), 3.0)
End Function
End Class
DoubleParameterizedFunctional F As New MyFunction()
This code encapsulates the same function using a DoubleVectorParameterizedDelegate:
Code Example – C# nonlinear least squares surface fit
public double MyFunction( DoubleVector p, DoubleVector x )
{
// z = ayx^2 + bsin(x) + cy^3
return p[0] * x[0] * Math.Pow( x[1], 2.0 ) +
p[1] * Math.Sin( x[0] ) +
p[2] * Math.Pow( x[1], 3.0 );
}
var f = new DoubleVectorParameterizedDelegate( MyFunction );
Code Example – VB nonlinear least squares surface fit
Public Function MyFunction(P As DoubleVector, X As DoubleVector) As
Double
Return P(0) * Math.Pow(X(0), 2.0) * X(1) +
P(1) * Math.Sin(X(0)) +
P(2) * Math.Pow(X(1), 3.0)
End Function
Dim F As New DoubleVectorParameterizedDelegate( MyFunction )
Constructing a MultiVariableFunctionFitter
Class MultiVariableFunctionFitter is templatized on INonlinearLeastSqMinimizer, and class BoundedMultiVariableFunction is templatized on IBoundedNonlinearLeastSqMinimizer (Section 32.1). Instances are constructed from an encapsulated generalized multivariable function. For example:
Code Example – C# nonlinear least squares surface fit
Func<DoubleVector, DoubleVector, double> myDelegate =
delegate( DoubleVector p, DoubleVector x )
{
// z = ayx^2 + bsin(x) + cy^3
return p[0] * x[0] * Math.Pow( x[1], 2.0 ) +
p[1] * Math.Sin( x[0] ) +
p[2] * Math.Pow( x[1], 3.0 );
};
DoubleVectorParameterizedDelegate f =
new DoubleVectorParameterizedDelegate( myDelegate );
MultiVariableFunctionFitter<TrustRegionMinimizer> fitter =
new MultiVariableFunctionFitter<TrustRegionMinimizer>( f );
Again, an existing minimizer instance can also be passed to the constructor:
Code Example – C# nonlinear least squares surface fit
var minimizer = new LevenbergMarquardtMinimizer();
minimizer.DefaultTolerance = 1e-6;
var fitter =
new MultiVariableFunctionFitter<LevenbergMarquardtMinimizer>(
f, minimizer );
Code Example – VB nonlinear least squares surface fit
Dim Minimizer As New LevenbergMarquardtMinimizer()
Minimizer.GradientTolerance = "1e-6"
Dim Fitter As New MultiVariableFunctionFitter(
Of LevenbergMarquardtMinimizer)(F, Minimizer)
Once you've constructed an instance of MultiVariableFunctionFitter or BoundedMultiVariableFunctionFitter containing a function, you can fit that function to a set of points using the Fit() method.
The Fit() method on MultiVariableFunctionFitter takes a DoubleMatrix of x values, where each row in the matrix represents a point, a DoubleVector of y values representing the data points, and a starting position in the function parameter space. For instance:
Code Example – C# nonlinear least squares surface fit
var x = new DoubleMatrix(10, 2);
x[Slice.All, 0] = new DoubleVector("3.6 7.7 9.3 4.1 8.6
2.8 1.3 7.9 10.0 5.4");
x[Slice.All, 1] = new DoubleVector("16.5 150.6 263.1 24.7 208.5
9.9 2.7 163.9 325.0 54.3");
var y = new DoubleVector("95.09 23.11 60.63 48.59 89.12
76.97 45.68 1.84 82.17 44.47");
var start = new DoubleVector("10 10 10");
DoubleVector solution = fitter.Fit( x, y, start );
Code Example – VB nonlinear least squares surface fit
Dim X As New DoubleMatrix(10, 2)
X(Slice.All, 0) = New DoubleVector("3.6 7.7 9.3 4.1 8.6" & _
"2.8 1.3 7.9 10.0 5.4")
X(Slice.All, 1) = New DoubleVector("16.5 150.6 263.1 24.7 208.5" & _
"9.9 2.7 163.9 325.0 54.3")
Dim Y As New DoubleVector("95.09 23.11 60.63 48.59 89.12" & _
"76.97 45.68 1.84 82.17 44.47")
Dim Start As New DoubleVector("10 10 10")
Dim Solution As DoubleVector = Fitter.Fit(X, Y, Start)
In the space of the function parameters, beginning at a specified start point, Fit() finds a minimum (possibly local) in the sum of the squared residuals with respect to the given x and y values.
NOTE—You must supply at least as many data points to fit as your function has parameters.
The Fit() method on BoundedMultiVariableFunctionFitter additionally accepts linear bounds on the solution:
Code Example – C# nonlinear least squares surface fit
var lowerBounds = new DoubleVector( "[0 -18 0]" );
var upperBounds = new DoubleVector( "[.007 -3 1]" );
DoubleVector solution =
fitter.Fit( x, y, start, lowerBounds, upperBounds );
Code Example – VB nonlinear least squares surface fit
Dim LowerBounds As New DoubleVector("[0 -18 0]")
Dim UpperBounds As New DoubleVector("[.007 -3 1]")
Dim Solution As DoubleVector =
Fitter.Fit(X, Y, Start, LowerBounds, UpperBounds)
Trying different initial starting points is recommended for better solutions. If possible, use starting points based on a priori information about the curve shape and the data being fit. Otherwise, random value close to zero are usually a good choice.
The Fit() method returns the solution found by the minimization. To compute the residuals relative to the data points at the solution, use the ResidualVector() method:
Code Example – C# nonlinear least squares surface fit
DoubleVector residuals = fitter.ResidualVector( x, y, solution );
Code Example – VB nonlinear least squares surface fit
Dim Residuals As DoubleVector =
Fitter.ResidualVector(X, Y, solution)
Additional information about the last performed fit is available from the underlying minimizer instance, accessible using the Minimizer property. For example, this code gets the sum of the squared residuals at the starting point and at the solution, the number of iterations performed, and the stop criterion:
Code Example – C# nonlinear least squares surface fit
INonlinearLeastSqMinimizer minimizer = fitter.Minimizer;
double initialResidual = minimizer.InitialResidual;
double finalResidual = minimizer.FinalResidual;
int iterations = minimizer.Iterations;
Code Example – VB nonlinear least squares surface fit
Dim Minimizer As INonlinearLeastSqMinimizer = Fitter.Minimizer
Dim InitialResidual As Double = Minimizer.InitialResidual
Dim FinalResidual As Double = Minimizer.FinalResidual
Dim Iterations As Integer = Minimizer.Iterations
