13.4 Polynomials (.NET, C#, CSharp, VB, Visual Basic, F#)
Class Polynomial extends OneVariableFunction (Section 13.1).
Rather than encapsulating an arbitrary function delegate, Polynomial represents a polynomial by
its coefficients, arranged in ascending order—that is, a vector
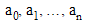such that:
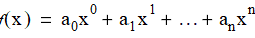
Thus, the polynomial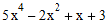 
is represented as a DoubleVector
of length 5 with elements "3
1 -2 0 5".
A Polynomial instance can be constructed in two ways. If you know the exact form of the polynomial, simply pass in the vector of coefficients:
Code Example – C# polynomials
var coef = new DoubleVector( "1 0 2"); // 2x^2 + 1
var p = new Polynomial( coef );
Code Example – VB polynomials
Dim Coef As New DoubleVector("1 0 2") ' 2x^2 + 1
Dim P As New Polynomial(Coef)
Alternatively, you can interpolate a polynomial through
a set of points. If the number of points is n,
then the constructed polynomial will have degree n
- 1 and pass through the interpolation points. For example, this code
interpolates the polynomial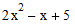 
through the points (1,6), (2,11),
and (3,20):
Code Example – C# polynomials
var x = new DoubleVector( "1 2 3");
var y = new DoubleVector( "6 11 20" );
var p = new Polynomial( x, y );
Code Example – VB polynomials
Dim X As New DoubleVector("1 2 3")
Dim Y As New DoubleVector("6 11 20")
Dim P As New Polynomial(X, Y)
You can also construct a Polynomial instance from a vector of x-values and a OneVariableFunction evaluated at each x:
Code Example – C# polynomials
var f = new Func<double, double>( myFunction );
var x = new DoubleVector( 10, 1, 1 );
var p = new Polynomial( x, f );
Code Example – VB polynomials
Dim F As New Func(Of Double, Double)(AddressOf myFunction)
Dim X As New DoubleVector(10, 1, 1)
Dim P As New Polynomial(X, F)
Class Polynomial inherits Function, Integrator, and Differentiator properties from OneVariableFunction (Section 13.1). Additionally, Polynomial provides these properties:
● Coeff gets and sets the vector of coefficients.
● Degree gets the degree of the polynomial.
The degree is the order of the highest non-zero coefficient. Therefore, the degree may be less than the length of the underlying coefficient vector, as returned for example by Coeff.Length. The Reduce() method is provided for removing trailing zeros from the coefficient vector.
Class Polynomial
inherits the Evaluate() method from OneVariableFunction. This method evaluates
a polynomial at a given x-value, or
vector of x
Code Example – C# polynomials
var coeff = new DoubleVector( "6 -1 5 0 3 -2" );
var p = new Polynomial( coeff );
double y = p.Evaluate( 1.25 );
Code Example – VB polynomials
Dim Coeff As New DoubleVector("6 -1 5 0 3 -2")
Dim P As New Polynomial(Coeff)
Dim Y As Double = P.Evaluate(1.25)
Algebraic Manipulation of Polynomials
Because a Polynomial is-a OneVariableFunction, all of the overloaded arithmetic operators and equivalent named methods described in Section 13.1 accept polynomials. For example, this code adds a Polymomial to a OneVariableFunction to create a new OneVariableFunction:
Code Example – C# polynomials
var coeff = new DoubleVector( "1 4 -1 1 2 -3" );
var p = new Polynomial( coeff );
var d = new Func<double, double>( MyFunction );
var f = new OneVariableFunction( d );
OneVariableFunction g = p + f;
Code Example – VB polynomials
Dim Coeff As New DoubleVector("1 4 -1 1 2 -3")
Dim P As New Polynomial(Coeff)
Dim D As New Func(Of Double, Double)(AddressOf MyFunction)
Dim F As New OneVariableFunction(D)
Dim G As Func(Of Double, Double) = P + F
Additionally, class Polynomial provides overloads of the arithmetic operators and named methods. These operators and methods work either with two polynomials, or with a polynomial and a scalar. They operate directly on the underlying vector(s) of coefficients, and therefore return instances of Polynomial. For example:
Code Example – C# polynomials
var coeff = new DoubleVector( "-11 3 1 1 0 -1 2" );
var p = new Polynomial( coeff );
Polynomial p2 = p/2;
Polynomial p3 = p + p2;
Code Example – VB polynomials
Dim Coeff As New DoubleVector("-11 3 1 1 0 -1 2")
Dim P As New Polynomial(Coeff)
Dim P2 As Polynomial = P / 2.0
Dim P3 As Polynomial = P + P2
NOTE—You can divide one Polynomial by another, but the result is a OneVariableFunction rather than a Polynomial, since the quotient is a rational function, and not necessarily a polynomial.
Class Polynomial inherits the Integrate() method from OneVariableFunction (Section 13.2), which computes the integral of the current function over a given interval. Polynomial also extends the interface to include an AntiDerivative() method that returns a new polynomial encapsulating the antiderivative (indefinite integral) of the current polynomial. For example:
Code Example – C# polynomials
var p = new Polynomial( new DoubleVector( "5 3 0 2" ) );
double integral = p.Integrate( -1, 1 );
Polynomial i = p.AntiDerivative();
Code Example – VB polynomials
Dim P As New Polynomial(New DoubleVector("5 3 0 2"))
Dim Integral As Double = P.Integrate(-1, 1)
Dim I As Polynomial = P.AntiDerivative()
In constructing the antiderivative, the constant of integration is assumed to be zero.
Each Polynomial object has a PolynomialIntegrator associated with it, which implements the IIntegrator interface. Because the antiderivative of a polynomial can be easily constructed, PolynomialIntegrator simply constructs the antiderivative and evaluates it at the lower and upper bounds. This gives the exact integral.
NOTE—You can, of course, set the IIntegrator associated with a Polynomial to a non-default value, such as a Romberg numerical integrator. But since this would only compute an approximation of the integral, there would be little point.
Class Polynomial inherits both Differentiate() and Derivative() methods from OneVariableFunction (Section 13.3). Differentiate() returns the derivative of the current function at a given x-value. Derivative() is overridden to return a new polynomial that is the first derivative of the current polynomial. Thus:
Code Example – C# polynomials
var coeff = new DoubleVector( "1 -2 3" );
var p = new Polynomial( coeff );
Polynomial der = p.Derivative(); // der.Coeff = "-2 6"
Code Example – VB polynomials
Dim Coeff As New DoubleVector("1 -2 3")
Dim P As New Polynomial(Doeff)
Dim Der As Polynomial = P.Derivative() ' Der.Coeff = "-2 6"
Each Polynomial object has a PolynomialDifferentiator associated with it, which implements the IDifferentiator interface. Because the derivative of a polynomial can be easily constructed, PolynomialDifferentiator simply constructs the first derivative and evaluates it at the given x-value. This gives the exact derivative.
NOTE—You can, of course, set the Differentiator associated with a polynomial to a non-default value, such as a Ridders numerical differentiator. But again, as this would only compute an approximation of the derivative, there would be little point.