NMath User's Guide

TOC | Previous | Next | Index

13.2 Numerical Integration (.NET, C#, CSharp, VB, Visual Basic, F#)

Numerical integration, also called quadrature, computes an approximation of the integral of a function over some interval. There are many methods for numerically evaluating integrals. NMath provides two of the most widely used, general purpose families of methods: Romberg integration, and Gauss-Kronrod integration.

NOTE—Class Polynomial provides a method for constructing the exact antiderivative of a polynomial. See Section 13.4 for more information.

Computing Integrals

The Integrate() method on OneVariableFunction (Section 13.1) computes the integral of a function over a given interval. For example, if f is a OneVariableFunction, this code integrates f over the interval -1 to 1:

Code Example – C# calculus

double integral = f.Integrate( -1, 1 );

Code Example – VB calculus

Dim Integral As Double = F.Integrate(-1, 1)

NOTE—NMath does not directly support improper intervals; that is, it must be possi­ble to evaluate the function at both the lower and upper bounds, and at any point in between (no singularities).

To perform integration, every OneVariableFunction has an IIntegrator object associated with it. NMath integration classes such as RombergIntegrator and GaussKronrodIntegrator implement the IIntegrator interface. The default integrator for a OneVariableFunction is an instance of RombergIntegrator, which may be changed using the Integrator property. Thus:

Code Example – C# calculus

f.Integrator = new GaussKronrodIntegrator();

double integral = f.Integrate( 0, Math.PI );

Code Example – VB calculus

F.Integrator = New GaussKronrodIntegrator()

Dim Integral As Double = F.Integrate(0, Math.PI)

You can also change the default IIntegrator associated with all instances of OneVariableFunction using the static DefaultIntegrator property. For instance:

Code Example – C# calculus

OneVariableFunction.DefaultIntegrator =

  new GaussKronrodIntegrator();





var d = new Func<double, double>( MyFunction );




var f = new OneVariableFunction( d );








double integral = f.Integrate( 0, 1 );  // uses Gauss-Kronrod








Code Example – VB calculus


OneVariableFunction.DefaultIntegrator = New 
GaussKronrodIntegrator()








Dim D As New Func(Of Double, Double)(AddressOf MyFunction)




Dim F As New OneVariableFunction(D)








Dim Integral As Double = f.Integrate(0, 1) ' uses Gauss-Kronrod 




Romberg Integration


In general, the class of methods known as Newton-Cotes formulas estimate
the integral of a function over a given interval by dividing the interval
into 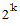 panels, where k is called the order,
estimating the integral within each panel, then summing the estimates.
For instance, the trapezoidal rule approximates
the function in each panel by a straight line between the end points.
Simpson's rule approximates
the function in two adjacent panels by a quadratic function connecting
the two outer points and the common midpoint. Higher-level methods are
obtained by interpolating higher degree polynomial segments.


Because all methods evaluate the function at the same
set of points, higher-level approximations can be derived from lower-level
approximations. For example, it can be shown that a kth-order
Simpson's rule approximation can be derived from two trapezoidal rule
approximations of order k and k-1. Similarly, a Boole's rule approximation,
which fits third-degree polynomials through the points associated with
four-panel partitions of the interval, can be derived from two Simpson's
rule approximations of order k and
k-1. In this way, all higher level
approximations can be derived from a series of trapezoidal rule approximations.


This iterated application of trapezoidal rule approximations
is known as Romberg integration. Romberg
integration is a very powerful method for quickly and accurately integrating
smooth functions.


In NMath, instances
of class RombergIntegrator compute
successive Romberg approximations of increasing order until the estimated
error in the approximation is less than a specified error tolerance,
or until the maximum order is reached. The default error tolerance is
1e-8, and the default maximum order is 20.


To perform integration, every OneVariableFunction
has an IIntegrator object associated
with it, which is used by the Integrate()
method to compute integrals. The default IIntegrator for a OneVariableFunction is an instance of
RombergIntegrator. For example, assuming f is a OneVariableFunction,
this code uses the default RombergIntegrator
to integrate over the interval -1 to 1:


Code Example – C# calculus


double estimate = f.Integrate( -1, 1);




Code Example – VB calculus


Dim Estimate As Double = f.Integrate(-1, 1)




The underlying IIntegrator
can be accessed using the Integrator property.


In some cases, you may wish to create a RombergIntegrator yourself. This gives
you more control over the integration process, and allows you to reuse
a customized integrator to integrate several functions, or one function
over several intervals. Thus, this code instantiates a RombergIntegrator, uses the provided
Tolerance property to change the error tolerance
and the MaximumOrder property to change
the maximum order, then calls the Integrate()
method on RombergIntegrator to
integrate functions f and g:


Code Example – C# calculus


var rom = new RombergIntegrator();




rom.Tolerance = 1e-6;




rom.MaximumOrder = 16;




double integralF = rom.Integrate( f, -1, 1);




double integralG = rom.Integrate( g, 0, 2 * Math.PI );




Code Example – VB calculus


Dim Rom As New RombergIntegrator()




Rom.Tolerance = "1e-6"




Rom.MaximumOrder = 16




Dim IntegralF As Double = Rom.Integrate(f, -1, 1)




Dim IntegralG As Double = Rom.Integrate(g, 0, 2 * Math.PI)




To compute a Romberg estimate of a specific order,
k, you can also set the MaximumOrder to k
and the Tolerance to a negative value. This
code configures the RombergIntegrator
to compute an 8th-order approximation:



Code Example – C# calculus


var rom = new RombergIntegrator();




rom.Tolerance = -1;




rom.MaximumOrder = 8;




double estimate = rom.Integrate( f, -1, 1);




Code Example – VB calculus


Dim Rom = New RombergIntegrator()




Rom.Tolerance = -1




Rom.MaximumOrder = 8




Dim Estimate As Double = Rom.Integrate(f, -1, 1)




After computing an estimate, a RombergIntegrator
holds a record of the iteration process. Read-only properties are provided
for accessing this information:


● RombergEstimate gets the Romberg estimate for
the integral, as returned by the Integrate()
method.


● RombergErrorEstimate gets an estimate of the error
in the Romberg estimate of the integral just computed.


● ToleranceMet returns true
if the estimate of the error in the Romberg approximation just computed
is less than or equal to the tolerance; otherwise, false.
(Integration ends either when the estimated error in the approximation
is less than tolerance, or when the maximum order is reached.)


● Order gets the order of the Romberg approximation
just computed.


● TrapeziodEstimate gets the estimate for the integral
yielded by the compound trapeziod rule where the number of panels is
equal to the order of the Romberg estimate.


● SimpsonEstimate gets the estimate for the integral
yielded by the compound Simpson's rule where the number of panels is
equal to the order of the Romberg estimate. (Note: Returns 0 if Order = 0.)


● Tableau gets the entire DoubleMatrix
of successive approximations computed while computing a Romberg estimate.
The rows are the order of approximation. The columns are the level of
approximation. The first column contains the trapezoidal approximations,
the second column the Simpson's rule approximations, the third column
the Boole's rule approximations, and so on, up to the Order
of the approximation just computed.


Thus, this code retrieves the Boole's rule approximation:


Code Example – C# calculus


var rom = new RombergIntegrator();




double integral = rom.Integrate( f, 0, 1);




int order = rom.Order;




DoubleMatrix tableau = rom.Tableau;








double boole;




if ( order >= 2 )




{




  boole = tableau[ order, 2 ];




}




Code Example – VB calculus


Dim Rom As New RombergIntegrator()




Dim Integral As Double = Rom.Integrate(f, 0, 1)




Dim Order As Integer = Rom.Order




Dim Tableau As DoubleMatrix = Rom.Tableau








Dim Boole As Double




If Order >= 2 Then




  Boole = Tableau(Order, 2)




End If




Gauss-Kronrod Integration


Gaussian
integration estimates an integral by evaluating the function at non-equally spaced points over the interval.
The method attempts to pick optimal points at which to evaluate the function,
and furthermore to weight the contribution of each point. Gauss-Kronrod integration is an adaptive
Gaussian quadrature method in which the function is evaluated at special
points known as Kronrod points. The
Gauss-Kronrod method is especially suited for non-singular oscillating
integrands.


NMath includes
Gauss-Kronrod classes for different numbers of Kronrod points (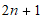, beginning with a Gauss 10-point
rule):


● GaussKronrod21Integrator approximates
integrals using the Gauss 10-point and the Kronrod 21-point
rule.


● GaussKronrod43Integrator approximates
integrals using the Gauss 21-point and the Kronrod 43-point
rule.


● GaussKronrod87Integrator approximates
integrals using the Gauss 43-point and the Kronrod 87-point
rule.


Finally, the automatic GaussKronrodIntegrator class
uses Gauss-Kronrod rules with increasing number of points. Approximation
ends when the relative error is less than the tolerance scaled by the
integration result, or when the maximum number of points is reached.
The default error tolerance is 1e-7; the
default maximum number of points is 87.
Unless you have reason to believe in advance that a particular Gauss-Kronrod
rule is optimal for your function, it is recommended that you use the
automatic integrator.


By default, OneVariableFunction
objects use RombergIntegrator objects
to compute integrals, but this may be changed using the Integrator property. For instance:


Code Example – C# calculus


f.Integrator = new GaussKronrodIntegrator();




double integral = f.Integrate( 0, Math.PI );




Code Example – VB calculus


F.Integrator = New GaussKronrodIntegrator()




Dim Integral As Double = F.Integrate(0, Math.PI)




This code specifically uses the GaussKronrod43Integrator,
rather than the automatic GaussKronrodIntegrator:


Code Example – C# calculus


f.Integrator = new GaussKronrod43Integrator();




double integral = f.Integrate( -1, 1 );




Code Example – VB calculus


F.Integrator = New GaussKronrod43Integrator()




Dim Integral As Double = F.Integrate(-1, 1)




In some cases you may wish to create a Gauss-Kronrod
integrator yourself. This gives you more control over the integration
process, and allows you to reuse a customized integrator to integrate
several functions, or one function over several intervals. Thus, this
code instantiates a GaussKronrodIntegrator, uses
the provided Tolerance property to change
the error tolerance, then calls the Integrate()
method on GaussKronrodIntegrator to
integrate functions f and g:


Code Example – C# calculus


var gk = new GaussKronrodIntegrator();




gk.Tolerance = 1e-6;




double integralF = gk.Integrate( f, -1, 1);




double integralG = gk.Integrate( g, 0, 2 * Math.PI );




Code Example – VB calculus


Dim GK As New GaussKronrodIntegrator()




GK.Tolerance = "1e-6"




Dim IntegralF As Double = GK.Integrate(f, -1, 1)




Dim IntegralG As Double = GK.Integrate(g, 0, 2 * Math.PI)




Read-only properties are provided for accessing information
about an integral approximation, once it has been computed: 


● RelativeErrorEstimate gets an estimate of the
relative error for the integral approximation.


● ToleranceMet gets a boolean value indicating whether
or not the relative error for the integral approximation is less than
the tolerance scaled by the integration result.


● PreviousEstimate gets the integral approximation
calculated using the previous rule—for example, the Gauss 10-point
rule for a GaussKronrod21Integrator,
the Kronrod 21-point rule for a GaussKronrod43Integrator,
and so forth.


For instance, this code checks whether the error tolerance
was met before proceeding:


Code Example – C# calculus


var gk = new GaussKronrodIntegrator();




gk.Tolerance = 1e-6;




double integral = gk.Integrate( f, -1, 1 );








if ( gk.ToleranceMet )




{




  // Do something here...




}




Code Example – VB calculus


Dim GK As New GaussKronrodIntegrator()




GK.Tolerance = "1e-6"




Dim Integral As Double = GK.Integrate(f, -1, 1)








If GK.ToleranceMet Then




  ' Do something here...




End If







Top

		


		
	

		

	


	



Top