33.2 Finding Function Roots of Derivable Functions (.NET, C#, CSharp, VB, Visual Basic, F#)
Class NewtonRalphsonRootFinder implements the IOneVariableDRootFinder interface and finds roots of univariate functions using the Newton-Raphson Method. The Newton-Raphson algorithm finds the slope of the function at the current point and uses the zero of the tangent line as an estimate of the root.
Like SecantRootFinder and RiddersRootFinder (Section 33.1), instances of NewtonRalphsonRootFinder are constructed by specifying an error tolerance and a maximum number of iterations, or by accepting the defaults for these values. For example:
Code Example – C# root finding
double tol = 1e-8;
int maxIter = 100;
var finder = new NewtonRaphsonRootFinder( tol, maxIter );
Code Example – VB root finding
Dim Tol As Double = "1e-8"
Dim MaxIter As Integer = 100
Dim Finder As New NewtonRaphsonRootFinder(Tol, MaxIter)
Once you have constructed a NewtonRalphsonRootFinder instance, you can use the Find() method to find a root within a given interval. For instance, this polynomial has a root at 1:
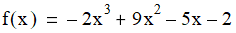
This code finds the root in the interval (0, 3):
Code Example – C# root finding
var p = new Polynomial(
new DoubleVector( -2.0, -5.0, 9.0, -2.0 ) );
var finder = new NewtonRaphsonRootFinder();
double lower = 0;
double upper = 3;
double root = finder.Find( p, p.Derivative(), lower, upper );
Code Example – VB root finding
Dim P As New Polynomial(New DoubleVector(-2.0, -5.0, 9.0, -2.0))
Dim Finder As New NewtonRaphsonRootFinder()
Dim Lower As Double = 0
Dim Upper As Double = 3
Dim Root As Double = Finder.Find(P, P.Derivative(), Lower, Upper)
