Chapter 48. Partial Least Squares (.NET, C#, CSharp, VB, Visual Basic, F#)
Partial Least Squares (PLS) is a technique that generalizes and combines features from principal component analysis (Section 46.1) and multiple linear regression (Chapter 42). It is particularly useful when you need to predict a set of response (dependent) variables from a large set of predictor (independent variables).
As in multiple linear regression, the goal of PLS regression is to construct a linear model
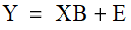
where Y is n cases by m variables response matrix, X is a n cases by p variables predictor matrix, B is a p by m regression coefficients matrix, and E is a noise term for the model which has the same dimensions as Y.
As in principal components regression, PLS regression produces factor scores as linear combinations of the original predictor variables, so that there is no correlation between the factor score variables used in the predictive regression model. For example, suppose that we have a matrix of response variables Y, and a large number of predictive variables X (in matrix form), some of which may be highly correlated. A regression using factor extraction for this data computes the score matrix T=XW for an appropriate matrix of weights W, and then considers the linear regression model Y=TQ+E, where Q is a matrix of regression coefficient, called loadings, for T, and E is an error term. Once the loadings Q are computed, the above regression model is equivalent to Y=XB+E, with B=WQ, which can be used as a predictive model.
PLS regression differs from principal components regression in the methods used for extracting factor scores. While principal components regression computes the weight matrix W reflecting the covariance structure between predictor variables, PLS regression produces the weight matrix W reflecting the covariance structure between the predictor and response variables.
For establishing the model with c factors, or components, PLS regression produces a p by c weight matrix W for X such that T=XW. These weights are computed so that each of them maximizes the covariance between responses and the corresponding factor scores. Ordinary least squares regression of Y on T are then performed to produce Q, the loadings for Y (or weights for Y) such that Y=TQ+E. Once Q is computed, we have Y=XB+E, where B=WQ.
