48.6 Cross Validation (.NET, C#, CSharp, VB, Visual Basic, F#)
Cross validation is a model evaluation method which measures how well a model makes predictions for data that it has not already sees (as with residuals). To accomplish this, some of the data is removed before the model is constructed. Once the model is constructed, the data that was removed can be used to test the performance of the model on the "new" data. The following methods are typically used:
● The Holdout Method
The simplest kind of cross validation is the holdout method. The data set is separated into two sets, called the training set and the testing set. The PLS regression is constructed using the training set, then the regression model is asked to make predictions for the responses for the predictor data in the training set. The errors it makes are accumulated to give the mean square error.
● K-fold Cross Validation
In k-fold cross validation, the data set is divided into k subsets, and the holdout method is repeated k times. Each time one of the k subsets is used as the test set and the other k-1 subsets are put together to form a training set. The average mean square error is then computed across all k trials.
● Leave-One-Out Cross Validation
Leave-one-out cross validation is the result of taking k-fold cross validation to its logical extreme, with k equal to n, the number of data points in the set. That means that n separate times, the PLS model is computed using all the data except for one point and a prediction is made for that point. As before the average mean square error is computed and used to evaluate the model.
NMath Stats provides two classes for doing k-fold cross validation on PLS models. PLS1CrossValidation is used when the response data is univariate, and PLS2CrossValidation is used when the response data is multivariate. To perform a cross validation calculation, you need to specify the data (Section 48.1), a PLS calculation algorithm (Section 48.5), and an algorithm for dividing the data into subsets.
To specify how subsets for k-fold cross validation are generated from the data, you must provide the cross validation class with an object implementing the ICrossValidationSubsets interface. NMath Stats provides classes LeaveOneOutSubsets, which implement the leave-one-out strategy, and KFoldSubsets, which implements k-fold with arbitrary k.
The average mean square error for the cross validation calculation is available as a property on the cross validation object. Also available is an array of PLS1CrossValidationResult or PLS2CrossValidationResult objects. Each result object contains testing and training data that was used for each cross validation calculation and the associated mean square error.
Jackknifing of Regression Coefficients
NMath Stats also provides class PLS2CrossValidationWithJackknife for evaluation of multivariate PLS models with model coefficient variance estimates and confidence intervals.
The jackknife estimator of a parameter is found by systematically leaving out each observation from a dataset and calculating the estimate and then finding the average of these calculations. Given a sample of size N, the jackknife estimate is found by aggregating the estimates of each N-1 estimate in the sample.
The original Tukey jackknife variance estimator is defined as
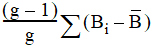
where g is the number
of subsets used in cross validation, 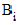 is the estimated
coefficients when subset i is left
out (called the jackknife replicates),
and
is the estimated
coefficients when subset i is left
out (called the jackknife replicates),
and 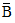 is the
mean of the
is the
mean of the 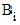 .
.
However, Martens and Martens (2000) defined the estimator as
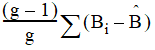
where 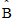 is the coefficient estimate using the entire data set—that
is, they use the original fitted coefficients instead of the mean of
the jackknife replicates. This is the default for class PLS2CrossValidationWithJackknife, but
you can set UseMean to true
for the original Tukey definition. For example:
is the coefficient estimate using the entire data set—that
is, they use the original fitted coefficients instead of the mean of
the jackknife replicates. This is the default for class PLS2CrossValidationWithJackknife, but
you can set UseMean to true
for the original Tukey definition. For example:
Code Example – C# PLS cross-validation with jackknife
int numComponents = 2;
var cv = new PLS2CrossValidationWithJackknife
{
Scale = false,
UseMeans = true
};
cv.DoCrossValidation( X, Y, numComponents );
Console.WriteLine( cv.CoefficientVariance );
Code Example – VB PLS cross-validation with jackknife
Dim NumComponents As Integer = 2
Dim CV As New PLS2CrossValidationWithJackknife
CV.Scale = False
CV.UseMeans = True
CV.DoCrossValidation(X, Y, NumComponents)
Console.WriteLine(CV.CoefficientVariance)
