30.1 Objective and Constraint Function Classes (.NET, C#, CSharp, VB, Visual Basic, F#)
Nonlinear and quadratic programming problems seek to minimize an objective function, subject to a set of constraint functions. NMath provides classes for encapsulating these functions, used by both QP and NLP solvers.
Two classes support objective functions:
● Class DoubleFunctional is an abstract class which derives from DoubleMultiVariableFunction. It is a particular type of multivariable function, where the dimension of the range space is one. Deriving classes must implement the Evaluate() method, and may optionally provide a Gradient() method.
● Since it is sometimes convenient to specify the objective function and its corresponding gradient using delegates (including anonymous delegates and lambda expressions), class DoubleFunctionalDelegate derives from DoubleFunctional and provides an easy way to wrap delegates in a DoubleFunctional interface. Thus, all functions which take a DoubleFunctional argument are overloaded to take a delegate argument.
For example, this code sub-classes DoubleFunctional to encapsulate an objective function:
Code Example – C#
// f(x) = exp(x0)*(4*x0^2 + 2*x1^2 + 4*x0*x1 + 2*x1 + 1)
class MyObjectiveFunction : DoubleFunctional
{
// Constructor. Must initilialize the base class with the
// dimension of the domain--2 in this case.
public ObjectiveFunction()
: base( 2 )
{}
public override double Evaluate( DoubleVector x )
{
double x0 = x[0];
double x1 = x[1];
return Math.Exp( x0 ) * ( 4 * x0 * x0 + 2 * x1 * x1 + 4 * x0 *
x1 + 2 * x1 + 1 );
}
public override void Gradient( DoubleVector x,
DoubleVector grad )
{
double x0 = x[0];
double x1 = x[1];
double ex0 = Math.Exp( x0 );
grad[0] = ex0 * ( 4 * x0 * x0 + 2 * x1 * x1 + 4 * x0 * x1 + 2 *
x1 + 1 ) + ex0 * ( 8 * x0 + 4 * x1 );
grad[1] = ex0 * ( 4 * x0 + 4 * x1 + 2 );
}
}
Code Example – VB
' f(x) = exp(x0)*(4*x0^2 + 2*x1^2 + 4*x0*x1 + 2*x1 + 1)
Public Class MyObjectiveFunction
Inherits DoubleFunctional
' Constructor. Must initilialize the base class with the
' dimension of the domain--2 in this case.
Public Sub New()
MyBase.New(2)
End Sub
Public Overrides Function Evaluate(X As DoubleVector) As Double
Dim X0 As Double = X(0)
Dim X1 As Double = X(1)
Return Math.Exp(X0) * (4 * X0 * X0 + 2 * X1 * X1 + 4 * X0 *
X1 + 2 * X1 + 1)
End Function
Public Overrides Sub Gradient(X As DoubleVector, Grad As DoubleVector)
Dim X0 = X(0)
Dim X1 = X(1)
Dim EX0 = Math.Exp(X0)
Grad(0) = EX0 * (4 * X0 * X0 + 2 * X1 * X1 + 4 * X0 * X1 + 2 *
X1 + 1) + EX0 * (8 * X0 + 4 * X1)
Grad(1) = EX0 * (4 * X0 + 4 * X1 + 2)
End Sub
End Class
This code uses a DoubleFunctionalDelegate:
Code Example – C#
public double MyFunction( DoubleVector x )
{
// f(x) = -x0 * x1 *x2
return -x[0] * x[1] * x[2];
}
int xDim = 3;
Func<DoubleVector, double> functional = MyFunction;
var objective = new DoubleFunctionalDelegate( xDim, functional )
Code Example – VB
Public Function MyFunction(X As DoubleVector) As Double
' f(x) = -x0 * x1 *x2
Return -X(0) * X(1) * X(2)
End Function
Dim XDim As Integer = 3
Dim Functional As New Func(Of DoubleVector, Double
(AddressOf MyFunction)
Dim Objective As New DoubleFunctionalDelegate(XDim, Functional)
NMath provides two concrete constraint classes: LinearConstraint and NonlinearConstraint, which both derive from the abstract base class Constraint. Constraint objects contain a constraint function c(x) and a constraint type, either equality or inequality, specified using the ConstraintType enumeration.
NOTE—It is assumed that equality type constraints have their constraint function c(x) equal to zero, and inequality type constraints have their constraint function c(x) greater than or equal to zero.
A linear constraint on a set of variables is a constraint upon a linear combination of those variables. LinearConstraint supports to two such constraints: equality constraints and lower bound constraints. That is, given variables x0, x1,..., xn and constants b, a0, a1,..., an, two types of constraints may be formed
a0*x0 + a1*x1 + . . . + an*xn = b
and
a0*x0 + a1*x1 + . . . + an*xn >= b
Upper bound constraints are represented as negations of lower bound constraints.
Nonlinear constraints
are of the form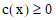 
(inequality constraint), or 
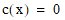(equality constraint),
where c(x) is a real-valued, smooth
function of the vector variable. Constraints can also be constructed
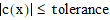with a tolerance. Equality constraints are satisfied when 
; inequality constraints
are satisfied when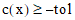 
.
In most cases, you will not need to create constraint objects directly. QP and NLP problem classes provide methods for adding constraints which construct the necessary constraint objects for you.