NMath User's Guide

TOC | Previous | Next | Index

45.6 Wilcoxon Signed-Rank Test (.NET, C#, CSharp, VB, Visual Basic, F#)

The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test for comparing the means between two paired samples, or repeated measurements on a single sample. It can be used as an alternative to TwoSamplePairedTTest when the population cannot be assumed to be normally distributed.

Class WilcoxonSignedRankTest tests if two paired sets of observed values differ from each other in a significant way. The null hypothesis is that the distribution x - y is symmetric about 0.

Creating Wilcoxon Signed-Rank Objects

A WilcoxonSignedRankTest instance is constructed from paired vectors of sample data.

Code Example – C# Wilcoxon signed-rank test

var a = new DoubleVector( 78, 24, 64, 45, 64, 52, 30, 50, 64, 50, 

  78, 22, 84, 40, 90, 72 );

var b = new DoubleVector( 78, 24, 62, 48, 68, 56, 25, 44, 56, 40, 

  68, 36, 68, 20, 58, 32 );





double alpha = 0.05;




var type = HypothesisType.TwoSided;




bool exactPValue = false;




var test =




  new WilcoxonSignedRankTest( a, b, alpha, type, exactPValue  );




Code Example – VB Wilcoxon signed-rank
test


TODO


Note that paired observations where either value is
missing, or where the difference between values is zero, are ignored.
In the example above, a normal approximation is used to compute p-value.
For 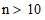, the sampling distribution of the
test statistic converges to a normal distribution. For smaller sample
sizes, an exact p-value can be calculated by enumerating all possible
combinations of the test statistic given n.


Code Example – C# Wilcoxon signed-rank
test


var x = new DoubleVector( 1.83, 0.50, 1.62, 2.48, 1.68, 1.88, 1.55, 




  3.06, 1.30 );




var y = new DoubleVector( 0.878, 0.647, 0.598, 2.050, 1.060, 1.290, 




  1.060, 3.140, 1.290 );








alpha = 0.01;




exactPValue = true;




test =




  new WilcoxonSignedRankTest( x, y, alpha, type, exactPValue );




Code Example – VB Wilcoxon signed-rank
test


TODO


An InvalidArgumentException
is raised if the given data contains zero valid pairs (valid pairs are
non-NaN and unequal), or if an exact p-value is specified for .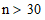






Top

		


		
	

		

	


	



Top