26.2 Minimizing Functions Without Calculating the Derivative (.NET, C#, CSharp, VB, Visual Basic, F#)
NMath provides two classes that implement the IOneVariableMinimizer interface, and minimize a OneVariableFunction using only function evaluations:
● Class GoldenMinimizer performs a golden section search for a minimum of a function, by successively narrowing an interval know to contain a local minimum. The golden section search method is linearly convergent.
● Class BrentMinimizer uses Brent's Method to minimize a function. Brent's Method combines golden section search with parabolic interpolation. Parabolic interpolation fits a parabola through the current set of points, then uses the parabola to estimate the function's minimum. The faster parabolic interpolation is used wherever possible, but in steps where the projected minimum falls outside the interval, or when successive steps are becoming larger, Brent's Method resorts back to the slower golden section search. Brent's Method is quadratically convergent.
Instances of GoldenMinimizer and BrentMinimizer are constructed by specifying an error tolerance and a maximum number of iterations, or by accepting the defaults for these values. For example, this code constructs a GoldenMinimizer using the default tolerance and a maximum of 50 iterations:
Code Example – C# minimization
int maxIter = 50;
var minimizer = new GoldenMinimizer( maxIter );
Code Example – VB minimization
Dim MaxIter As Integer = 50
Dim Minimizer As New GoldenMinimizer(MaxIter)
Instances of GoldenMinimizer and BrentMinimizer provide Minimize() methods for minimizing a given function within a given interval. Overloads of Minimize() accept a bounding Interval, a Bracket, or a triplet of points satisfying the bracketing conditions (Section 26.1). For example, the function
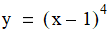
has a minimum at 1.0. To compute the minimum, first encapsulate the function:
Code Example – C# minimization
public static double MyFunction( double x )
{
return Math.Pow( x - 1, 4 );
}
var f = new OneVariableFunction(
new Func<double, double>( MyFunction ) );
Code Example – VB minimization
Public Shared Function MyFunction(X As Double) As Double
Return Math.Pow(X - 1, 4)
End Function
Dim F As New OneVariableFunction(
New Func(Of Double, Double)(AddressOf MyFunction))
This code finds a minimum of f in the interval (0,2) using golden section search:
Code Example – C# minimization
var minimizer = new GoldenMinimizer();
int lower = 0;
int upper = 2;
double min = minimizer.Minimize( f, lower, upper );
Code Example – VB minimization
Dim Minimizer As New GoldenMinimizer()
Dim Lower As Integer = 0
Dim Upper As Integer = 2
Dim Min As Double = Minimizer.Minimize(F, Lower, Upper)
This code first constructs a Bracket starting from (0,10), then finds a minimum of f using Brent's Method:
Code Example – C# minimization
double tol = 1e-9;
int maxIter = 25;
var minimizer = new BrentMinimizer( tol, maxIter );
var bracket = new Bracket( f, 0, 10 );
double min = minimizer.Minimize( bracket );
Code Example – VB minimization
Dim Tol As Double = "1e-9"
Dim MaxIter As Integer = 25
Dim Minimizer As New BrentMinimizer(Tol, MaxIter)
Dim Bracket As New Bracket(F, 0, 10)
Dim Min As Double = Minimizer.Minimize(Bracket)
