6.7 Functions of Matrices (.NET, C#, CSharp, VB, Visual Basic, F#)
NMath provides a variety of functions that take matrices as arguments.
The matrix classes provide Transpose() member functions for calculating the transpose of a matrix: B[i,k] = A[k,i]. Class NMathFunctions also provides a static Transpose() method that returns the transpose of a matrix. For instance:
Code Example – C# matrix
var A = new FloatComplexMatrix( 5, 5, 1, 1 );
FloatComplexMatrix B = A.Transpose();
FloatComplexMatrix C = NMathFunctions.Transpose(A);
// B == C
Code Example – VB matrix
Dim A As New FloatComplexMatrix(5, 5, 1.0F, 1.0F)
Dim B As FloatComplexMatrix = A.Transpose()
Dim C As FloatComplexMatrix = NMathFunctions.Transpose(A)
' B == C
In both cases, the matrix returned is a new view of the same data. Transpose() just swaps the number of rows and the number of columns, as well as the row strides and column strides. No data is copied.
The matrix classes provide member functions OneNorm() to compute the 1-norm (or largest column sum) of a matrix, InfinityNorm() to compute the infinity-norm (or largest row sum) of a matrix, and FrobeniusNorm() to compute the Frobenius norm. For instance:
Code Example – C# matrix
var A = new DoubleMatrix( "3x3 [1 2 3 4 5 6 7 8 9]" );
double d1 = A.OneNorm();
double d2 = A.InfinityNorm();
Code Example – VB matrix
Dim A As New DoubleMatrix("3x3 [1 2 3 4 5 6 7 8 9]")
Dim D1 As Double = A.OneNorm()
Dim D2 As Double = A.InfinityNorm()
Class NMathFunctions provides the static Product() method for calculating the matrix product of two matrices. For example:
Code Example – C# matrix
var A = new FloatMatrix( "3x3 [1 2 3 4 5 6 7 8 9]" );
var B = new FloatMatrix( 3, 3, 1, 1 );
FloatMatrix C = NMathFunctions.Product( A, B );
Code Example – VB matrix
Dim A As New FloatMatrix("3x3 [1 2 3 4 5 6 7 8 9]")
Dim B As New FloatMatrix(3, 3, 1.0F, 1.0F)
Dim C As FloatMatrix = NMathFunctions.Product(A, B)
Transpose operations to be performed on the operands of a matrix-matrix multiply operation are specified using a value from the NMathFunctions.ProductTransposeOption enum:
● TransposeNone does not transpose either matrix before multiplying.
● TransposeBoth transposes both operands before multiplying.
● TransposeFirst transposes only the first operand before multiplying.
● TransposeSecond transposes only the second operand before multiplying.
● ConjTransposeBoth takes the conjucate transpose of both operands before multiplying.
● ConjTransposeFirst takes the conjugate transpose only of the first operand before multiplying.
● ConjTransposeSecond takes the conjugate transpose only of the second operand before multiplying.
Thus, this code calculates the inner product of the transpose of A with B:
Code Example – C# matrix
var A = new FloatMatrix( "3x3 [1 2 3 4 5 6 7 8 9]" );
var B = new FloatMatrix( 3, 3, 1, 1 );
FloatMatrix C = NMathFunctions.Product( A, B,
ProductTransposeOption.TransposeFirst );
Code Example – VB matrix
Dim A As New FloatMatrix("3x3 [1 2 3 4 5 6 7 8 9]")
Dim B As New FloatMatrix(3, 3, 1.0F, 1.0F)
Dim C As FloatMatrix = NMathFunctions.Product(A, B,
ProductTransposeOption.TransposeFirst)
Additional overloads of the Product() method calculate the inner product of a matrix and a scalar:
Code Example – C# matrix
var A = new DoubleMatrix( "3x3 [1 2 3 4 5 6 7 8 9]" );
var v = new DoubleVector( "[3 2 1]" );
DoubleVector u = NMathFunctions.Product( A, v );
Code Example – VB matrix
Dim A As New DoubleMatrix("3x3 [1 2 3 4 5 6 7 8 9]")
Dim V As New DoubleVector("[3 2 1]")
Dim U As DoubleVector = NMathFunctions.Product(A, V)
Overloads are also provided which place the result of multiplying the first two operands into a third argument, rather than allocating new memory for the result:
Code Example – C# matrix
NMathFunctions.Product( A, B, C,
ProductTransposeOption.TransposeBoth );
Code Example – VB matrix
NMathFunctions.Product(A, B, C,
ProductTransposeOption.TransposeBoth)
Matrix Inverse and Pseudoinverse
Class NMathFunctions provides the static Inverse() method for calculating the inverse of a matrix:
Code Example – C# matrix
var A = new FloatMatrix( "3x3 [1 2 3 4 5 6 7 8 9]" );
FloatMatrix AInv = NMathFunctions.Inverse( A );
Code Example – VB matrix
Dim A As New FloatMatrix("3x3 [1 2 3 4 5 6 7 8 9]")
Dim AInv As FloatMatrix = NMathFunctions.Inverse(A)
The standard inverse fails if the matrix is singular or not square.
The pseudoinverse
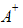 is a generalization of the
inverse, and exists for any n x m matrix, where
is a generalization of the
inverse, and exists for any n x m matrix, where 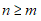 :
:
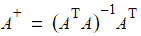
NMathFunctions provides the static Pseudoinverse() method:
Code Example – C# matrix
FloatMatrix APseudoInv = NMathFunctions.Pseudoinverse( A );
Code Example – VB matrix
Dim APseudoInv As FloatMatrix = NMathFunctions.PseudoInverse(A)
To test the quality of the pseudoinverse, you can check
the condition number of 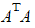 :
:
Code Example – C# matrix
float cond = NMathFunctions.ConditionNumber(
NMathFunctions.TransposeProduct( A, A ), NormType.OneNorm );
if (cond > 0.000001)
{
// good
}
Code Example – VB matrix
Dim Cond As Single = NMathFunctions.ConditionNumber(
NMathFunctions.TransposeProduct(A, A), NormType.OneNorm)
If Cond > 0.000001 Then
' good
End If
NOTE—The best way to compute the pseudoinverse is to use singular value decomposition. Method MatrixFunctions.Pseudoinverse() implements this method.
Class NMathFunctions provides static methods for rounding the elements of a matrix:
● Round() rounds each element of a given matrix to the specified number of decimal places.
● Ceil() applies the ceiling rounding function to each element of a given matrix.
● Floor() applies the floor rounding function to each element of a given matrix.
The static Sum() method on NMathFunctions accepts a matrix and returns a vector containing the sums of the elements in each column. To sum the rows, simply Transpose() the matrix first.
For example:
Code Example – C# matrix
var A = new DoubleMatrix( 5, 8, 1, 1 );
DoubleVector AColSums = NMathFunctions.Sum( A );
DoubleVector ARowSums = NMathFunctions.Sum( A.Transpose() );
A.Transpose() // return A to original view
Code Example – VB matrix
Dim A As New DoubleMatrix(5, 8, 1.0, 1.0)
Dim AColSums As DoubleVector = NMathFunctions.Sum(A)
Dim ARowSums As DoubleVector = NMathFunctions.Sum(A.Transpose())
A.Transpose() ' return A to original view
Transpose() just swaps the number of rows and the number of columns, as well as the row strides and column strides. No data is copied.
NaNSum() ignores values that are Not-A-Number (NaN).
NOTE—NaN functions are available for real-value matrices only, not complex number matrices.
The static Delta() method on NMathFunctions returns a new matrix with the same dimensions as a given matrix, whose values are the result of applying the vector delta function to each column of the matrix. The vector delta computes the differences between successive elements in a given vector, such that:
u[0] = v[0]
u[i] = v[i] - v[i-1]
Applied to a matrix, Delta() returns a new matrix such that:
B[0,j] = A[0,j]
B[i,j] = A[i,j] - A[i-1,j]
Again, to apply the Delta() function to rows rather than columns, just transpose the matrix first.
Class NMathFunctions provides static min/max finding methods that return a vector containing the value of the element in each column that meets the appropriate criterion:
● Max() returns a vector containing the greatest values in each column.
● Min() returns a vector containing the smallest values in each column.
● NaNMax() returns a vector containing the greatest values in each column, ignoring values that are Not-a-Number (NaN).
● NaNMin() returns a vector containing the smallest values in each column.
NOTE—NaN functions are available for real-value matrices only, not complex number matrices.
To apply these functions to the rows of a matrix, simply Transpose() the matrix first.
The static Mean(), Median(), Variance(), and SumOfSquares() methods on NMathFunctions are overloaded to accept a matrix and return a vector containing the result of applying the appropriate function to each column in the matrix:
Code Example – C# matrix
var A = new FloatMatrix( 5, 5, 0, 2 );
FloatVector means = NMathFunctions.Mean( A );
FloatVector medians = NMathFunctions.Median( A );
FloatVector variances = NMathFunctions.Variance( A );
Code Example – VB matrix
Dim A As New FloatMatrix(5, 5, 0.0F, 2.0F)
Dim Means As FloatVector = NMathFunctions.Mean(A)
Dim Medians As FloatVector = NMathFunctions.Median(A)
Dim Variances As FloatVector = NMathFunctions.Variance(A)
NaNMean(), NaNMedian(), NaNVariance(), and NaNSumOfSquares() ignore values that are Not-A-Number (NaN). NaNCount() returns the number of NaN values in each column. NaN functions are available for real-value matrices only, not complex matrices.
To apply these functions to the rows of a matrix, simply Transpose() the matrix first.
NMath extends standard trigonometric functions Acos(), Asin(), Atan(), Cos(), Cosh(), Sin(), Sinh(), Tan(), and Tanh() to take matrix arguments. Class NMathFunctions provides these functions as static methods. For instance, this code construct a matrix whose contents are the sines of another matrix:
Code Example – C# matrix
var A = new FloatMatrix( 10, 10, 0, Math.Pi/4 );
FloatMatrix cosA = NMathFunctions.Cos( A );
Code Example – VB matrix
Dim A As New FloatMatrix(10, 10, 0.0F, Math.PI / 4.0F)
Dim CosA As FloatMatrix = NMathFunctions.Cos(A)
The static Atan2() method takes two matrices and applies the two-argument arc tangent function to corresponding pairs of elements.
NMath extends standard transcendental functions Exp(), Log(), Log10(), and Sqrt() to take matrix arguments. Class NMathFunctions provides these functions as static methods; each takes a single matrix as an argument and return a matrix as a result. For example, this code creates a matrix whose elements are the square root of the elements in another matrix:
Code Example – C# matrix
var A = new DoubleMatrix( 3, 3, 1, 1 );
DoubleMatrix sqrt = NMathFunctions.Sqrt( A );
Code Example – VB matrix
Dim A As New DoubleMatrix(3, 3, 1.0, 1.0)
Dim Sqrt As DoubleMatrix = NMathFunctions.Sqrt(A)
Function Expm() on NMathFunctions raises the constant e to a given matrix power, using a scaling and squaring method based upon Pade approximation. This is different than method Exp() which exponentiates each element of a matrix independently.
Class NMathFunctions also provides the exponential function Pow() to raise each element of a matrix to a real exponent.
Code Example – C# matrix
var A = new DoubleMatrix( "2x2 [1 2 3 4]" );
DoubleMatrix cubed = NMathFunctions.Pow( A, 3 );
Code Example – VB matrix
Dim A As New DoubleMatrix("2x2 [1 2 3 4]")
Dim Cubed As DoubleMatrix = NMathFunctions.Pow(A, 3)
Absolute Value and Square Root
The static Abs() function on class NMathFunctions applies the absolute value function to each element of a given matrix:
Code Example – C# matrix
var A = new DoubleMatrix( 10, 10, 0, -1 );
DoubleMatrix abs = NMathFunctions.Abs( A );
Code Example – VB matrix
Dim A As New DoubleMatrix(10, 10, 0.0, -1.0)
Dim Abs As DoubleMatrix = NMathFunctions.Abs(A)
NMath also extends the standard Sqrt() function to take a matrix argument. Thus, this code creates a matrix whose elements are the square root of another matrix's elements:
Code Example – C# matrix
var A = new FloatMatrix( 10, 10, 1, 2 );
FloatMatrix sqrt = NMathFunctions.Sqrt( A );
Code Example – VB matrix
Dim A As New FloatMatrix(10, 10, 1.0F, 2.0F)
Dim Sqrt As FloatMatrix = NMathFunctions.Sqrt(A)
The static SortByColumn() method on class NMathFunctions sorts the rows of a matrix by the values in a specified column. For instance, this code sorts matrix A by values in the first column:
Code Example – C# matrix
var A = new FloatMatrix( 20, 20, 0, 1 );
A = NMathFunctions.SortByColumn( A, 0 );
Code Example – VB matrix
Dim A As New FloatMatrix(20, 20, 0.0F, 1.0F)
A = NMathFunctions.SortByColumn(A, 0)
Static methods Real() and Imag() on class NMathFunctions return the real and imaginary part of the elements of a matrix. If the elements of the given matrix are real, Real() simply returns the given matrix and Imag() returns a matrix of the same dimensions containing all zeros.
Static methods Arg() and Conj() on class NMathFunctions return the arguments (or phases) and complex conjugates of the elements of a matrix. If the elements of the given matrix are real, both methods simply return the given matrix.
For instance:
Code Example – C# matrix
DoubleComplexMatrix A =
new DoubleComplexMatrix( "2x2 [(1,-1) (2,-.5) (2.2,1.1) (7,9)]" );
DoubleComplexMatrix AConj = NMathFunctions.Conj( A );
// AConj = 2x2 [(1,1) (2,0.5) (2.2,-1.1) (7,-9)]
// Now use the Imag method to create a real matrix containing
// the imaginary parts of AConj.
DoubleMatrix AConjImag = NMathFunctions.Imag( AConj );
Code Example – VB matrix
Dim A As New DoubleComplexMatrix(
"2x2 [(1,-1) (2,-.5) (2.2,1.1) (7,9)]")
Dim AConj As DoubleComplexMatrix = NMathFunctions.Conj(A)
' AConj = 2x2 [(1,1) (2,0.5) (2.2,-1.1) (7,-9)]
' Now use the Imag method to create a real matrix containing
' the imaginary parts of AConj.
Dim AConjImag As DoubleMatrix = NMathFunctions.Imag(AConj)
