41.6 Two Sample F-Test (.NET, C#, CSharp, VB, Visual Basic, F#)
Class TwoSampleFTest tests whether the variances of two populations are equal. For example, suppose random samples from two normal populations are taken. The first sample consists of 10 observations with a standard deviation of 5.203; the second sample consists of 25 observations with a standard deviation of 2.623. At the 0.10 significance level, is there sufficient evidence to suggest that the populations from which these samples were drawn have equal variances?
As described Section 41.1,
all hypothesis test classes provide two paths for constructing instances
of that type: a parameter-based method and a data-based method. Thus,
you can construct a TwoSampleFTest
object by explicitly specifying the standard deviation (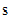
),and size (
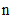) of each sample, like
so:
Code Example – C# F-test
double s1 = 5.203;
int n1 = 10;
double s2 = 2.623;
int n2 = 25;
var test = new TwoSampleFTest( s1, n1, s2, n2 );
Code Example – VB F-test
Dim S1 As Double = 5.203
Dim N1 As Integer = 10
Dim S2 As Double = 2.623
Dim N2 As Integer = 25
Dim Test As New TwoSampleFTest(S1, N1, S2, N2)
Or by supplying two sets of sample data. For instance, if the sample data is in two vectors v1 and v2:
Code Example – C# F-test
var test = new TwoSampleFTest( v1, v2 );
Code Example – VB F-test
Dim Test As New TwoSampleFTest(V1, V2)
The sample standard deviations and sizes are calculated from the given data.
In addition to the properties common to all hypothesis test objects (Section 41.1), a TwoSampleFTest object provides the following read-only properties:
● S1 and S2 get the standard deviations of the samples.
● N1 and N2 get the sizes of the samples.
● DegreesOfFreedom1 gets the numerator degrees of freedom.
● DegreesOfFreedom2 gets the denomenator degrees of freedom.
By default, a TwoSampleFTest
object performs a two-sided hypothesis test (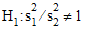
) with 
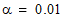. Non-default test parameters
can be specified at the time of construction using constructor overloads,
or after construction using the provided Type
and Alpha properties.
Once you've constructed and configured a TwoSampleFTest object, you can access the various test results using the provided properties, as described in Section 41.1:
Code Example – C# F-test
Console.WriteLine( "t-statistic = " + test.Statistic );
Console.WriteLine( "numerator df = " + test.DegreesOfFreedom1 );
Console.WriteLine( "denomenator df = " + test.DegreesOfFreedom2 );
Console.WriteLine( "p-value = " + test.P );
Console.WriteLine( "reject the null hypothesis? " + test.Reject);
Code Example – VB F-test
Console.WriteLine("t-statistic = " & Test.Statistic)
Console.WriteLine("numerator df = " & Test.DegreesOfFreedom1)
Console.WriteLine("denomenator df = " & Test.DegreesOfFreedom2)
Console.WriteLine("p-value = " & Test.P)
Console.WriteLine("reject the null hypothesis? " & Test.Reject)
The output is:
F-statistic = 3.93469497446923
numerator df = 9
denomenator df = 24
p-value = 0.00693561186501657
reject the null hypothesis? True
This indicates that we cannot reject the null hypotheses
(
).
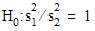Finally, remember that the ToString() method returns a formatted string representation of the complete test results:
Two Sample F Test
-----------------
Sample Sizes = 10 and 25
Standard Deviations = 5.203 and 2.623
Variances = 27.071209 and 6.880129
Computed F statistic: 3.93469497446923, num df = 9, denom df = 24
Hypothesis type: two-sided
Null hypothesis: true ratio of variances = 1
Alt hypothesis: true ratio of variances != 1
P-value: 0.00693561186501657
REJECT the null hypothesis for alpha = 0.01
0.99 confidence interval: 1.06490202325594 22.5425454339445