41.2 One Sample Z-Test (.NET, C#, CSharp, VB, Visual Basic, F#)
Class OneSampleZTest determines whether a sample from a normal distribution with known standard deviation could have a given mean. For example, suppose we wish to determine whether the IQs of children from a particular school are above average, given that Wechsler IQ scores are normally distributed with a mean of 100 and standard deviation of 15. Sample scores from 9 students are 116 110 111 113 112 113 111 109 121, with a mean of 112.8.
As described Section 41.1,
all hypothesis test classes provide two paths for constructing instances
of that type: a parameter-based method and a data-based method. Thus,
you can construct a OneSampleZTest
object by explicitly specifying a sample mean (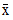
), sample size (
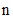), population mean (
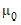), and population standard
deviation (
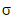), like
so:
Code Example – C# z-test
double xbar = 112.8;
int n = 9;
double mu0 = 100;
double sigma = 15;
var test = new OneSampleZTest( xbar, n, mu0, sigma );
Code Example – VB z-test
Dim XBar As Double = 112.8
Dim N As Integer = 9
Dim Mu0 As Double = 100
Dim Sigma As Double = 15
Dim Test As New OneSampleZTest(XBar, N, Mu0, Sigma)
Or by supplying a set of sample data, and the necessary population parameters:
Code Example – C# z-test
var data =
new DoubleVector( "[ 116 110 111 113 112 113 111 109 121 ]" );
double mu0 = 100;
double sigma = 15;
var test = new OneSampleZTest( data, mu0, sigma );
Code Example – VB z-test
Dim MYData As New DoubleVector("[ 116 110 111 113 112 113 111 109 121 ]")
Dim Mu0 As Double = 100
Dim Sigma As Double = 15
Dim Test As New OneSampleZTest(MyData, Mu0, Sigma)
In this case, the sample mean and sample size are calculated from the given data.
In addition to the properties common to all hypothesis test objects (Section 41.1), a OneSampleZTest object provides the following read-only properties:
● Xbar gets the sample mean.
● N gets the sample size.
● Mu0 gets the population mean.
● Sigma gets the population standard deviation.
By default, a OneSampleZTest
object performs a two-sided hypothesis test (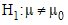
) with 
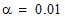. In this example, we
wish to test the one-sided form to the right (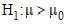
; that is, we wish to
test whether the children in our sample have a higher
than average IQ. Suppose also that we wish to set the alpha level to
0.05. Non-default test parameters can be
specified at the time of construction using constructor overloads, or
after construction using the provided Alpha
and Type properties, like so:
Code Example – C# z-test
test.Type = HypothesisType.Right;
test.Alpha = 0.05;
Code Example – VB z-test
Test.Type = HypothesisType.Right
test.Alpha = 0.05
Once you've constructed and configured a OneSampleZTest object, you can access the test results using the provided properties, as described in Section 41.1:
Code Example – C# z-test
Console.WriteLine( "z-statistic = " + test.Statistic );
Console.WriteLine( "p-value = " + test.P );
Console.WriteLine( "reject the null hypothesis? " + test.Reject);
Code Example – VB z-test
Console.WriteLine("z-statistic = " & Test.Statistic)
Console.WriteLine("p-value = " & Test.P)
Console.WriteLine("reject the null hypothesis? " & Test.Reject)
The output is:
z-statistic = 2.56
p-value = 0.00523360816355578
reject the null hypothesis? true
This indicates that we can reject the null hypotheses
(
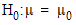). We can conclude
that the children have IQs significantly above average.
Finally, remember that the ToString() method returns a formatted string representation of the complete test results:
One Sample Z Test
-----------------
Sample mean = 112.8
Sample size = 9
Population mean = 100
Population standard deviation = 15
Computed Z statistic: 2.56
Hypothesis type: one-sided to the right
Null hypothesis: sample mean = population mean
Alt hypothesis: sample mean > population mean
P-value: 0.00523360816355578
REJECT the null hypothesis for alpha = 0.05
0.95 confidence interval: 104.575731865243 Infinity