49.1 Significance of the Overall Model (.NET, C#, CSharp, VB, Visual Basic, F#)
Class GoodnessOfFit tests the overall model significance for least squares model-fitting classes, such as LinearRegression, PolynomialLeastSquares, and OneVariableFunctionFitter.
GoodnessOfFit instances can be constructed from:
● A LinearRegression object.
● A PolynomialLeastSquares object, plus the vectors of x and y data.
● A OneVariableFunctionFitter object, plus the vectors of x and y data and the solution found by the fitter.
For example:
Code Example – C# goodness of fit
var x = new DoubleVector(0.3330, 0.1670, 0.0833, 0.0416,
0.0208, 0.0104, 0.0052);
var y = new DoubleVector(3.636, 3.636, 3.236, 2.660,
2.114, 1.466, 0.866);
int degree = 2;
var pls =
new PolynomialLeastSquares(degree, x, y);
var gof = new GoodnessOfFit(pls, x, y);
Code Example – VB goodness of fit
Dim X As New DoubleVector(0.333, 0.167, 0.0833, 0.0416, 0.0208,
0.0104, 0.0052)
Dim Y As New DoubleVector(3.636, 3.636, 3.236, 2.66, 2.114, 1.466,
0.866)
Dim Degree As Integer = 2
Dim PLS As New PolynomialLeastSquares(Degree, X, Y)
Dim GoF As New GoodnessOfFit(PLS, X, Y)
A variety of properties are provided for assessing the significance of the overall model:
● RegressionSumOfSquares gets the regression sum of squares. This quantity indicates the amount of variability explained by the model. It is the sum of the squares of the difference between the values predicted by the model and the mean.
● ResidualSumOfSquares gets the residual sum of squares. This is the sum of the squares of the differences between the predicted and actual observations.
● ModelDegreesOfFreedom gets the number of degrees of freedom for the model, which is equal to the number of predictors in the model.
● ErrorDegreesOfFreedom gets the number of degress of freedom for the model error, which is equal to the number of observations minus the number of model paramters.
● RSquared gets the coefficient of determination.
● AdjustedRsquared gets the adjusted coefficient of determination.
● MeanSquaredResidual gets the mean squared residual. This quantity is the equal to ResidualSumOfSquares / ErrorDegreesOfFreedom (equals the number of observations minus the number of model parameters).
● MeanSquaredRegression gets the mean squared for the regression. This is equal to RegressionSumOfSquares / ModelDegreesOfFreedom (equals the number of predictors in the model).
● FStatistic gets the overall F
statistic for the model. This is equal to the ratio of MeanSquaredRegression
/ MeanSquaredResidual. This is the statistic for the hypothesis
test where the null hypothesis, 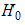 is that all the parameters are equal to 0
and the alternative hypothesis is that at least one paramter is nonzero.
is that all the parameters are equal to 0
and the alternative hypothesis is that at least one paramter is nonzero.
● FStatisticPValue gets the p-value for the F statistic.
For example, if lr is a LinearRegression object:
Code Example – C# goodness of fit
var gof = new GoodnessOfFit( lr );
double sse = gof.ResidualSumOfSquares;
double r2 = gof.RSquared;
double fstat = gof.FStatistic;
double fstatPval = gof.FStatisticPValue;
Code Example – VB goodness of fit
Dim GoF As New GoodnessOfFit(LR)
Dim SSE As Double = GoF.ResidualSumOfSquares
Dim R2 As Double = GoF.RSquared
Dim FStat As Double = GoF.FStatistic
Dim FStatPval As Double = GoF.FStatisticPValue
Lastly, the FStatisticCriticalValue() function computes the critical value for the F statistic at a given significance level:
Code Example – C# goodness of fit
double critVal = gof.FStatisticCriticalValue(.05);
Code Example – VB goodness of fit
Dim CritVal As Double = GoF.FStatisticCriticalValue(0.05)
