35.4 Stiff Equations (.NET, C#, CSharp, VB, Visual Basic, F#)
A stiff equation is a differential equation for which common numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. In NMath, class VariableOrderOdeSolver solves stiff and non-stiff ordinary differential equations. The algorithm uses higher order methods and smaller step size when the solution varies rapidly.
The Solve() method solves the given initial value problem of ordinary differential equation of the form
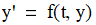
or
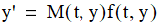
for problems that involve a mass matrix M.
The function takes
● A delegate which evaluates the right hand side of the differential equations.
● A timespan vector specifying the interval of integration [t0, tf]. The solver imposes initial conditions at t0 and integrates from t0 to tf. If the timespan vector contains two elements, the solver returns the solution evaluated at every integration step. If the timespan vector contains more than two points, the solver returns the solution evaluated at the given points. The time values must be in order, either increasing or decreasing.
● The initial value for problem—the value of the unknown function y at the initial time value.
For example, the van der Pol equations in relaxation oscillation provide an example of a stiff system.1 The limit cycle has portions where the solution components change slowly and the problem is quite stiff, alternating with regions of very sharp change where it is not stiff.
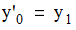
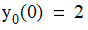
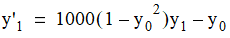
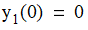
To simulate this system, first create a function containing
the equations. The following code creates the parameterized Van der Pol
equation with parameter 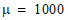 . Parameter t is the time value,
and y is the state value.
. Parameter t is the time value,
and y is the state value.
Code Example – C# stiff ODE solver
public static DoubleVector vdp1000( double t, DoubleVector y)
{
DoubleVector dy = new DoubleVector( 2 );
double y0 = y[0];
double y1 = y[1];
dy[0] = y1;
dy[1] = 1000 * ( 1 - (y0 * y0) ) * y1 - y0;
return dy;
}
Next, create a function that returns the Jacobian at given t and y values.
Code Example – C# stiff ODE solver
public static DoubleMatrix vdp1000Jac(double t, DoubleVector y)
{
DoubleMatrix J = new DoubleMatrix( 2, 2 );
J[0, 0] = 0;
J[0, 1] = 1;
J[1, 0] = -2 * 1000 * y[0] * y[1] - 1;
J[1, 1] = 1000 * ( 1.0 - y[0] * y[0] );
return J;
}
Create the initial values and time interval, and encapsulate the ODE function.
Code Example – C# stiff ODE solver
var y0 = new DoubleVector( 2.0, 0.0 );
var timespan = new DoubleVector( 0.0, 3000.0 );
var odeFunc =
new Func<double, DoubleVector, DoubleVector>( vdp1000 );
Create the solver object and set up the solver options. Here we use the default relative and absolute tolerances (1e-3 and 1e-6, respectively). Also, since we have an explicit form for the Jacobian function, we set this in the solver options too.
Code Example – C# stiff ODE solver
var ode15s = new VariableOrderOdeSolver();
var options = new VariableOrderOdeSolver.Options();
options.JacobianFunction =
new Func<double, DoubleVector, DoubleMatrix>( vdp1000Jac );
Finally, solve the equation and display the solution.
Code Example – C# stiff ODE solver
VariabeOrderOdeSolver.Solution<DoubleMatrix> soln =
ode15s.Solve( vdp1000, timespan, y0, options );
Console.WriteLine( "t = " + NMathFunctions.Round(soln.T, 4) );
Console.WriteLine();
Console.WriteLine( "y = " );
Console.WriteLine(
NMathFunctions.Round( soln.Y, 4 ).ToTabDelimited() );
