Savitzky-Golay smoothing effectively removes local signal noise while preserving the shape of the signal. Commonly, it’s used as a preprocessing step with experimental data, especially spectrometry data because of it’s effectiveness at removing random variation while minimally degrading the signal’s information content. Savitzky-Golay boils down to a fast (multi-core scaling) correlation operation, and therefore can be used in a real-time environment or on large data sets efficiently. If higher order information is needed from the signal, Savitzky-Golay can also provide high quality smoothed derivatives of a noisy signal.
Algorithm
Savitzky-Golay locally smooths a signal by fitting a polynomial, in a least squares sense, to a sliding window of data. The degree of the polynomial and the length of the sliding window are the filter’s two tuning parameters. If n is the degree of the polynomial that we are fitting, and k is the width of the sliding window, then
is needed for smoothing behavior (we must avoid an over-determined system). Typically
n is 3 or 4, and k depends on the size in samples of the noisy features to be suppressed in your data set.
For the case of n=0 the Savitzy-Golay filter degenerates to a moving average filter – which is good for removing white noise, but is poor for preserving peak shape (higher order moments). For n=1, the filter does a linear least-squares fit of the windowed data to a line. If n=k-1, the polynomial exactly fits data point in the window, and so no filtering takes place.
Once the polynomial is fit, then (typically) the center data-point in this window is replaced by value of the polynomial at that location. The window then slides to the right one sample and the process is repeated.
Savizky-Golay delivers the unexpected surprise that the polynomial fitting coefficients are constant for a given n and k. This means that once we fix n and k for our filter, the Savizky-Golay polynomial fitting coefficients are computed once during setup and then used across the entire data set. This is why Savizky-Golay is a high performance correlation filter.
Comparison Example
The following three images show some real experimental data and a comparison of two filtering algorithms. The first image shows the raw data, the second image shows the effect of an averaging filter, and the last image demonstrates a Savitzky-Golay smoothing filter of length five.
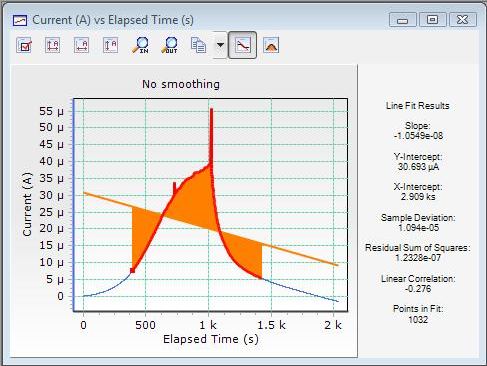
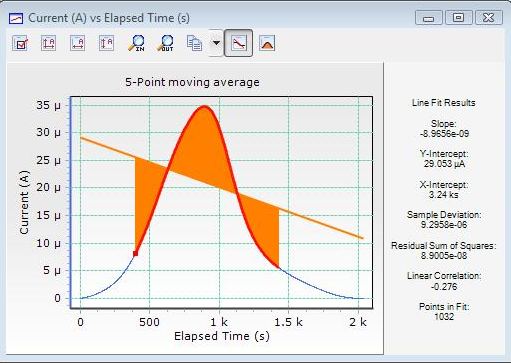
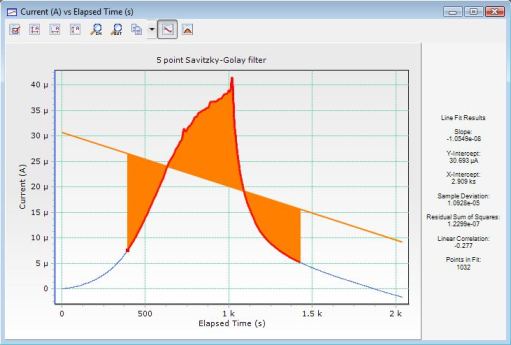
The averaging filter introduces a large error into the location of the orange peak whereas Savitzky-Golay removes the noise while maintaining the peak location. Computationally, they require identical effort.
Savitzky-Golay Smoothing in C#
The Savitzky-Golay smoothing filter is implemented in the NMath-Stats package as a generalized correlation filter. Any filter coefficients can be used with this moving window filter, Savitzky-Golay coefficients are just one possibility. The moving window filter also does not require the filtering to take place in the center of the sliding window; so when specifying the window, two parameters are required: number to the left, and number to the right of the filtered data point.
Here are the key software components.
- MovingWindowFilter.
SavitzkyGolayCoefficients(nLeft, nRight, PolyDeg) - MovingWindowFilter(nLeft, nRight, Coefficients[])
- MovingWindowFilter.Filter(data, boundary options)
The first is a static function for generating the Savizky-Golay coefficients, the second is the filtering class that takes the generated coefficients in the constructor. The third is the method that does the Savitzky-Golay filtering by running a cross-correlation between the data the the saved coefficients.
Below is a complete code example to copy and experiment with your own data sets. Only three lines of code are needed to build the filter and actually do the filtering. The remaining code builds a synthetic noisy signal to filter and displays the results.
int nLeft = 2;
int nRight = 2;
int n = 3;
// Generate the coefficients.
DoubleVector c =
MovingWindowFilter.SavitzkyGolayCoefficients( nLeft, nRight, n );
// Build the filter of width: nLeft + nRight + 1
MovingWindowFilter filter =
new MovingWindowFilter( nLeft, nRight, c );
Console.WriteLine( "Filter coeffs = " + filter.Coefficients );
// Generate a signal
DoubleVector x = new DoubleVector( 100, -5, .1 );
DoubleVector y = new DoubleVector( x.Length );
for ( int i = 0; i < x.Length; i++ )
{
double a = x[i];
y[i] = 0.03*Math.Pow(a, 3) + 0.2*Math.Pow(a, 2) -.22*a + 0.5;
}
Console.WriteLine( "Smoothed signal = " + y );
RandGenUniform rng = new RandGenUniform(-1, 1, 0x124 );
for ( int i = 0; i < y.Length; i++ )
{
y[i] += rng.NextDouble();
}
Console.WriteLine( "x = " + x );
Console.WriteLine( "Noisy signal = " + y );
// Do the filtering.
DoubleVector z =
filter.Filter(y, MovingWindowFilter.BoundaryOption.PadWithZeros);
Console.WriteLine( "Signal filtered = " + z );
-Paul
Addendum – Savitzky-Golay Coefficients
If you want to quickly try out Savitzky-Golay smoothing without computing the coefficients, or just compare coefficients, here are some coefficients for a sliding window of length five. They also provide some insight into the relationship between the coefficients and the behavior of the filter.
Filter length = 5, nLeft = 2, nRight = 2. Polynomial of order 0, [ 0.2 0.2 0.2 0.2 0.2 ] (averaging filter) Polynomial of order 1, [ 0.2 0.2 0.2 0.2 0.2 ] Polynomial of order 2, [ -0.0857142 0.3428571 0.4857142 0.3428571 -0.0857142 ] Polynomial of order 3, [ -0.0857142 0.3428571 0.4857142 0.3428571 -0.0857142 ] Polynomial of order 4 and higher, [ 0 0 1 0 0 ] (as expected, no filtering here!)
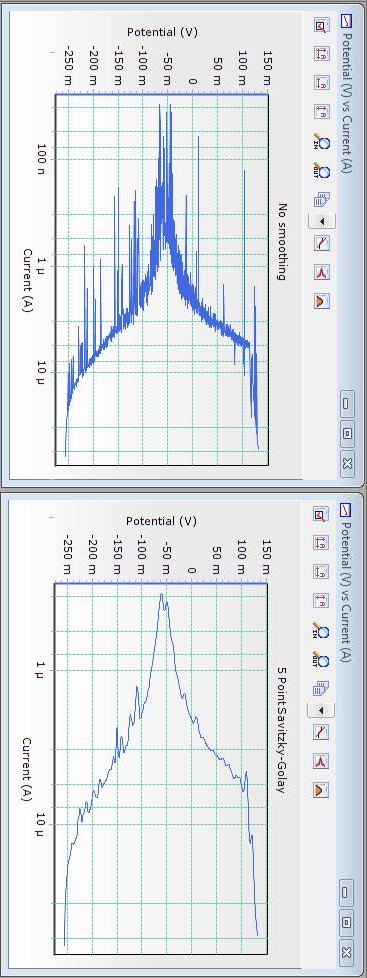
Another Smoothing Example on Real Data
This is another example of Savitzky-Golay smoothing on some experimental data. If more smoothing was desired, a longer filtering window could have been used.

Does your library have an appropriate function for performing similar filtering where the samples are not evenly spaced in x? The x dimension of my samples represents the position of a linear actuator when the sample was taken, but dynamic considerations require it to still be accelerating fairly substantially inside the area I am interested in measuring.
Oops, I should add the detail that because the samples are acquired at evenly spaced times and the actuator is accelerating or decelerating, the spacing between the positions at which they are acquired is uneven.
Hi Doug,
to smooth your measured x-displacements with a Savtizy-Golay filter you need data sampled at a fixed sample rate – which is exactly what you have. Fill a DoubleVector with your sampled data and apply your Savitzy-Golay filter. Have a look at this blog post to plot your results: https://www.centerspace.net/blog/nmath/net-math-with-microsoft-chart-controls-revisited/ .
Best,
Paul