26.3 Minimizing Derivable Functions (.NET, C#, CSharp, VB, Visual Basic, F#)
Class DBrentMinimizer implements the IOneVariableDMinimizer interface and minimizes a univariate function using Brent's Method in combination with evaluations of the first derivative. As described in Section 26.2, Brent's Method uses parabolic interpolation to fit a parabola through the current bracketing triplet, then uses the parabola to estimate the function's minimum. Class DBrentMinimizer uses the sign of the derivative at the central point of the bracketing triplet to decide which region should be used for the next test point.
Like GoldenMinimizer and BrentMinimizer (Section 26.2), instances of DBrentMinimizer are constructed by specifying an error tolerance and a maximum number of iterations, or by accepting the defaults for these values. This code constructs a DBrentMinimizer using the default error tolerance and maximum number of iterations:
Code Example – C# minimization
var minimizer = new DBrentMinimizer();
Code Example – VB minimization
Dim Minimizer As New DBrentMinimizer()
This code uses an error tolerance of 10-4 and a maximum of 50 iterations:
Code Example – C# minimization
double tol = 1e-4
int maxIter = 50;
var minimizer = new DBrentMinimizer( tol, maxIter );
Code Example – VB minimization
Dim Tol As Double = 0.0001
Dim MaxIter As Integer = 50
Dim Minimizer As New DBrentMinimizer(Tol, MaxIter)
Once you have constructed a DBrentMinimizer instance, you can use the Minimize() method to minimize a given function within a given interval. Overloads of Minimize() accept a bounding Interval, a Bracket, or a triplet of points satisfying the bracketing conditions (Section 26.1). Because DBrentMinimizer uses evaluations of the first derivative of the function, you must also supply a OneVariableFunction encapsulating the derivative. For example, the function:
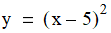
has a minimum at 5.0. To compute the minimum, first encapsulate the function and its derivative:
Code Example – C# minimization
public static double MyFunction( double x )
{
return ( ( x - 5 ) * ( x - 5 ) );
}
public static double MyFunctionPrime( double x )
{
return ( 2 * x ) - 10;
}
var f = new OneVariableFunction(
new Func<double, double>( MyFunction ) );
var df = new OneVariableFunction(
new Func<double, double>( MyFunctionPrime ) );
Code Example – VB minimization
Public Shared Function MyFunction(X As Double) As Double
Return ((x - 5) * (x - 5))
End Function
Public Shared Function MyFunctionPrime(X As Double) As Double
Return (2 * X) - 10
End Function
Dim F As New OneVariableFunction(
New Func(Of Double, Double)(AddressOf MyFunction))
Dim DF As New OneVariableFunction(
New Func(Of Double, Double)(AddressOf MyFunctionPrime))
This code then constructs a Bracket starting from (1,2), and computes the minimum:
Code Example – C# minimization
var minimizer = new DBrentMinimizer();
var bracket = new Bracket( f, 1, 2 );
double min = minimizer.Minimize( bracket, df );
Code Example – VB minimization
Dim Minimizer As New DBrentMinimizer()
Dim Bracket As New Bracket(F, 1, 2)
Dim Min As Double = Minimizer.Minimize(Bracket, DF)
