17.6 Tridiagonal Matrices (.NET, C#, CSharp, VB, Visual Basic, F#)
A tridiagonal matrix is a matrix which has
all its non-zero entries on the main diagonal, the superdiagonal, and
the subdiagonal. That is,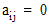 
whenever 
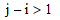or 
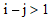. For example, this is a
5 x 5 tridiagonal matrix:
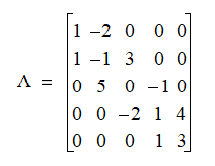
Tridiagonal matrices often occur in one-dimensional problems and at an intermediate stage in the process of finding eigenvalues.
NMath provides tridiagonal matrix classes for four datatypes: single- and double-precision floating point numbers, and single- and double-precision complex numbers. The classnames are FloatTriDiagMatrix, DoubleTriDiagMatrix, FloatComplexTriDiagMatrix, and DoubleComplexTriDiagMatrix.
For efficiency, zero elements outside the main diagonal, superdiagonal, and subdiagonal are not stored. A tridiagonal matrix is a special case of a banded matrix where the upper and lower bandwidths are one, and the storage scheme is the same as for a banded matrix (Section 17.5).