41.5 Two Sample Unpaired T-Test (.NET, C#, CSharp, VB, Visual Basic, F#)
Class TwoSampleUnpairedTTest tests whether two samples from a normal distribution could have the same mean when the standard deviations are unknown but assumed to be equal, allowing for a pooled estimate of the variance.
Class TwoSampleUnpairedUnequalTTest assumes that the samples may come from populations with unequal variances, and the Welch-Satterthwaite approximation to the degrees of freedom is used. Unlike TwoSampleUnpairedTTest, a pooled estimate of the variance is not used.
For example, suppose we work for a company that makes plastic widgets and we want to compare plastic samples from two suppliers for strength. We record the breaking strength in psi (pounds per square inch) for random samples from each supplier and obtain the following data: 11 samples from the first supplier having a mean strength of 4.2 psi and a standard deviation of 4.68; 8 samples from the second supplier have a mean strength of 5.6 and a standard deviation of 3.92.
As described Section 41.1,
all hypothesis test classes provide two paths for constructing instances
of that type: a parameter-based method and a data-based method. Thus,
you can construct a TwoSampleUnpairedTTest
object by explicitly specifying the mean (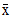
), standard deviation
(
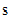), and size (
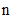) of each sample, like
so:
Code Example – C# unpaired t-test
double xbar1 = 4.2;
double s1 = 4.68;
int n1 = 11;
double xbar2 = 5.6;
double s2 = 3.92;
int n2 = 8;
var test = new TwoSampleUnpairedTTest( xbar1, s1, n1, xbar2, s2, n2 );
Code Example – VB unpaired t-test
Dim XBar1 As Double = 4.2
Dim S1 As Double = 4.68
Dim N1 As Integer = 11
Dim XBar2 As Double = 5.6
Dim S2 As Double = 3.92
Dim N2 As Integer = 8
Dim Test As New
TwoSampleUnpairedTTest(XBar1, S1, N1, XBar2, S2, N2)
Or by supplying two sets of sample data. For instance, if the sample data is in two vectors supplier1 and supplier2:
Code Example – C# unpaired t-test
var test =
new TwoSampleUnpairedTTest( supplier1, supplier2 );
Code Example – VB unpaired t-test
Dim Test As New TwoSampleUnpairedTTest(Supplier1, Supplier2)
The sample means, standard deviations, and sizes are calculated from the given data.
In addition to the properties common to all hypothesis test objects (Section 41.1), a TwoSampleUnpairedTTest object provides the following read-only properties:
● Xbar1 and Xbar2 get the means of the samples.
● S1 and S2 get the standard deviations of the samples.
● SPooled gets the pooled estimate of the standard deviation.
● N1 and N2 get the sizes of the samples.
● DegreesOfFreedom gets the degrees of freedom.
By default, a TwoSampleUnpairedTTest
object performs a two-sided hypothesis test (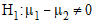
) with 
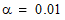. Non-default test parameters
can be specified at the time of construction using constructor overloads,
or after construction using the provided Type
and Alpha properties.
Once you've constructed and configured a TwoSampleUnpairedTTest object, you can access the various test results using the provided properties, as described in Section 41.1:
Code Example – C# unpaired t-test
Console.WriteLine( "t-statistic = " + test.Statistic );
Console.WriteLine( "pooled standard deviation = " + test.SPooled );
Console.WriteLine( "deg of freedom = " + test.DegreesOfFreedom );
Console.WriteLine( "p-value = " + test.P );
Console.WriteLine( "reject the null hypothesis? " + test.Reject);
Code Example – VB unpaired t-test
Console.WriteLine("t-statistic = " & Test.Statistic)
Console.WriteLine("pooled standard deviation = " & Test.SPooled)
Console.WriteLine("deg of freedom = " & Test.DegreesOfFreedom)
Console.WriteLine("p-value = " & Test.P)
Console.WriteLine("reject the null hypothesis? " & Test.Reject)
The output is:
t-statistic = -0.687410859118054
pooled standard deviation = 4.38304755647859
degrees of freedom = 17
p-value = 0.501095386120306
reject the null hypothesis? False
This indicates that we cannot reject the null hypotheses
(
).
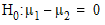Finally, remember that the ToString() method returns a formatted string representation of the complete test results:
Two Sample t Test (Unpaired)
----------------------------
Sample means = 4.2 and 5.6
Sample standard deviations = 4.68 and 3.92
Sample sizes = 11 and 8
Difference in means = -1.4
Pooled standard deviation = 4.38304755647859
Computed t statistic: -0.687410859118054, df = 17
Hypothesis type: two-sided
Null hypothesis: true difference in means = 0
Alt hypothesis: true difference in means != 0
P-value: 0.501095386120306
Decision: RETAIN the null hypothesis for alpha = 0.05
0.95 confidence interval: -5.69690885703539 2.8969088570354