13.1 Encapsulating Functions (.NET, C#, CSharp, VB, Visual Basic, F#)
Class OneVariableFunction encapsulates an arbitrary function, and works with other numerical classes to approximate integrals and derivatives.
NOTE—Class Polynomial extends OneVariableFunction, and provides exact methods for integration and differentiation of polynomials, as well as various convenience functions for creating and manipulating polynomials. This is the preferred class to use if your function is a polynomial. See Section 13.4 for more information.
Creating a Function of One Variable
A OneVariableFunction is constructed from a Func<double, double>, a function delegate that takes a single double parameter and returns a double.
For example, suppose you wish to encapsulate this function:
Code Example – C# calculus
public double MyFunction( double x )
{
return Math.Sin( x ) + Math.Pow( x, 3 ) / Math.PI;
}
Code Example – VB calculus
Function MyFunction(X As Double) As Double
Return Math.Sin(X) + Math.Pow(X, 3) / Math.PI
End Function
First, create a delegate for the MyFunction() method:
Code Example – C# calculus
var d = new Func<double, double>( MyFunction );
Code Example – VB calculus
Dim D As New Func(Of Double, Double)(AddressOf MyFunction)
Then construct a OneVariableFunction encapsulating the delegate:
Code Example – C# calculus
var f = new OneVariableFunction( d );
Code Example – VB calculus
Dim F As New OneVariableFunction(D)
A Func<double, double> delegate is also implicitly converted to a OneVariableFunction. Thus:
Code Example – C# calculus
OneVariableFunction f = d;
Code Example – VB calculus
OneVariableFunction f = d;
A OneVariableFunction object has the following properties:
● Function gets the encapsulated function delegate.
● Integrator gets and sets the integration object associated with the function (see Section 13.2).
● Differentiator gets and sets the differentiation object associated with the function (see Section 13.3).
The Evaluate() method on OneVariableFunction evaluates a function at a given x-value. For instance, if f is a OneVariableFunction:
Code Example – C# calculus
double y = f.Evaluate( Math.PI );
Code Example – VB calculus
Dim Y As Double = F.Evaluate(Math.PI)
Evaluate() also accepts a vector of x-values, and returns a vector of y-values, such that y[i] = f( x[i] ). Thus, this code evaluates f at 100 points between 0 and 1:
Code Example – C# calculus
var x = new DoubleVector( 100, 0, 1.0/100 );
DoubleVector y = f.Evaluate( x );
Code Example – VB calculus
Dim X As New DoubleVector(100, 0, 1.0 / 100.0)
Dim Y As DoubleVector = F.Evaluate(X)
Finally, Evaluate() accepts
another OneVariableFunction, and
returns a new function encapsulating the composite. For example, if f encapsulates the function 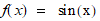 and g
encapsulates
and g
encapsulates 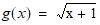 , you can create
a new function that encapsulates
, you can create
a new function that encapsulates 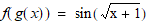 like so:
like so:
Code Example – C# calculus
OneVariableFunction composite = f.Evaluate( g );
Code Example – VB calculus
Dim Composite As OneVariableFunction = F.Evaluate(g)
Algebraic Manipulation of Functions
NMath provides overloaded arithmetic operators for functions with their conventional meanings for those .NET languages that support them, and equivalent named methods for those that do not. Table 10 lists the equivalent operators and methods.
Operator |
Equivalent Named Method |
+ |
Add() |
- |
Subtract() |
* |
Multiply() |
/ |
Divide() |
Unary - |
Negate() |
All binary operators and equivalent named methods work either with two functions, or with a function and a scalar. For example, this C# code uses the overloaded operators:
Code Example – C# calculus
OneVariableFunction g = f/2;
OneVariableFunction sum = f + g;
OneVariableFunction neg = -f;
This Visual Basic code uses the equivalent named methods:
Code Example – VB calculus
Dim G As OneVariableFunction = OneVariableFunction.Divide(F, 2)
Dim Sum As OneVariableFunction = OneVariableFunction.Add(F, g)
Dim Neg As OneVariableFunction = OneVariableFunction.Negate(F)
Finally, as a convenience, NMathFunctions provides a Pow() method that raises a function to a scalar power:
Code Example – C# calculus
OneVariableFunction g = NMathFunctions.Pow( f, 3.5 );
Code Example – VB calculus
Dim G As OneVariableFunction = NMathFunctions.Pow(F, 3.5)
