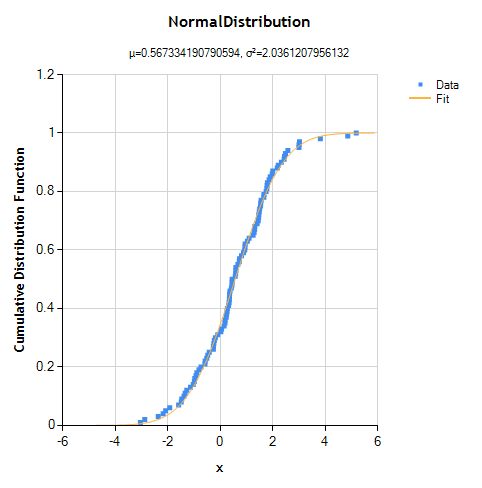
A customer recently asked how to fit a normal (Gaussian) distribution to a vector of experimental data. Here's a demonstration of how to do it.
Let's start by creating a data set: 100 values drawn from a normal distribution with known parameters (mean = 0.5, variance = 2.0).
int n = 100;
double mean = .5;
double variance = 2.0;
var data = new DoubleVector( n, new RandGenNormal( mean, variance ) )...
Read More
Read More
