Optimal Portfolio Allocation - CenterSpace Blog

The problem of optimal portfolio allocation, in its simplest form, asks the question of how to fully allocate a given amount of wealth across a fixed universe of investments to achieve a minimum-risk goal-expected return. The known quantities are the potential field of investments, their performance history, and the goal rate of return; The unknown is the wealth allocation across the investments. In this standard formulation, the phrase ‘minimum-risk’ is understood to be equivalent to ‘minimum-variance’ of the portfolio return. Said another way, in this model the investor will expect to get a ‘risk-premium’ (higher return) for investing in assets which have a higher historic return variance. This understanding of risk is at the heart of Harry Markowitz’s portfolio theory [5].

In the following brief development of optimal portfolio allocation theory we follow the paper by P. J. Atzberger [2]. If we have n investments we represent a fully invested portfolio as,

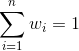
$\sum^{n}_{i=1}w_i = 1$

where the fraction of wealth invested in the i^th asset is w_i. We use this normalization to avoid working with the absolute magnitudes of the assets and resultant portfolios.

The rate of return of the entire portfolio, ρ_p at a given time t is,

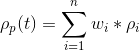
$\rho_p(t) = \sum^{n}_{i=1}w_i*\rho_i$

or simply the weighted sum of investment returns.

And because expectation is a linear operator, the expected rate of return of a given portfolio is,

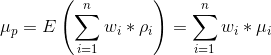
$\mu_p = E \left( \sum^{n}_{i=1}w_i*\rho_i \right ) = \sum^{n}_{i=1}w_i*\mu_i$

Where μ_i is expected rate of return of the i^th investment option.

And finally from the expected return of return, the portfolio variance will be given by,

$\sigma_p^2 = E \left( |\rho_p - \mu_p|^2 \right ) = \textbf{w}^T V \textbf{w}$

where w is the vector of normalized fractional investments defined above. (See eq. (13) in [2] for the full derivation). This is the minimum theoretical framework needed to setup the optimization problem.

Optimization with Markowitz Theory

Using our established problem framework we can cast the optimal portfolio allocation problem as a constrained quadratic optimization problem by minimizing the portfoilo’s variance (risk) subject to two linear constraints.

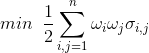
$min {\,\,\,} {1\over{2}} \sum^{n}_{i,j=1} \omega_i \omega_j \sigma_{i,j}$

subject to,

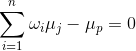
$\sum^{n}_{i=1} \omega_i \mu_j - \mu_p = 0$

and,

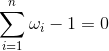
$\sum^{n}_{i=1} \omega_i - 1 = 0$

The minimized objective function is the variance of the portfolio – which is thought of as risk equivalent in this model. The first constraint insures that the built portfolio achieves a goal return of μ_p and the second constraint enforces the full allocation of wealth. There are many variants of this basic setup such as including a zero-risk investment (cash) to the pool of possible investments or adding constraints to allocate various percentages of wealth into different risk-classified investments [2][4].

Solving the Quadratic Programming Problem

This constrained optimization problem can be solved using NMath‘s quadratic programming class, ActiveSetQPSolver(). The basic steps of setting up the QP solver involve (1) Reading and parsing the investment data, (2) Setting up the problem constraints, (3) Executing the solve. The data for this example come from a data repository for exploring various Operations Research (OR) problems, run by J.E. Beasley. The specific data we study here has a universe of 225 potential assets, is found here, and is the largest test data set used in the paper “Heuristics for cardinality constrained portfolio optimisation” [3] (A brief description of the data set can be found on the same server here). The data set provides the basic information we need for optimizing the portfolio – the mean return and standard deviation of return of each investment and the correlation between all possible pairs of assets. The code to parse this file is appended to the end of this article.

Before generating the QP’s constraints we need to set up a QuadraticProgrammingProblem instance.

  // Set up QR problem using port5.txt data
  FloatMatrix covariance = correlation * 
                           ( NMathFunctions.Product( new FloatMatrix( stdDevReturn ), 
                           ( new FloatMatrix( stdDevReturn ).Transpose() ) ) );
  QuadraticProgrammingProblem problem = new QuadraticProgrammingProblem();
  problem.H = covariance;
  problem.c = new DoubleVector(n, 0);

First, the covariance matrix is computed from the investment standard deviations and correlations. Next we create and initialize a QuadraticProgrammingProblem instance. Since this QP solver class solves programs of the form: Minimize x'Hx + x'c, the c variable is set to zero.

The following code snippet sets up the QP constraints.

  ...
  QuadraticProgrammingProblem problem = new QuadraticProgrammingProblem();
  ...
  // Set up constraints
  LinearConstraint sumToOne = new LinearConstraint( 
                   new DoubleVector( n, 1 ), 1, ConstraintType.EqualTo );
  LinearConstraint returnRate = new LinearConstraint( 
                   meanReturn, targetReturn, ConstraintType.GreaterThanOrEqualTo );
  problem.AddConstraint( returnRate );
  problem.AddConstraint( sumToOne );

  // Add the bound on each var, w: w > 0
  for ( int i = 0; i < n; i++ )
    problem.AddLowerBound( i, 0.0 );

The first two constraints, sumToOne and returnRate were outlined above in the brief Markowitz theory section. The third constraint has been added to insure that we have a positive ownership in all assets; in this way we have disallowed shorting assets. This constraint can be deleted to include shorted asset in the optimized portfolio, if desired. All of these constraints are added to the QuadraticProgrammingProblem instance.

We can now put all of this together and solve the constrained 225 variable QP using the ActiveSetQPSolver class [0].

Asset   Allocation
   8,   0.0795
  39,   0.0866
  42,   0.0812
  59,   0.1201
  61,   0.2567
  96,   0.0593
 128,   0.0741
 170,   0.0573
 195,   0.0980
 214,   0.0688
 224,   0.0183
(All other assets have an allocation of zero.)

Total allocation:  1.0000
Total return-rate:  0.2000%, Target return-rate  0.2000%
Total solver time required:  0.1830 seconds

The optimal allocation includes 11 of our 225 investments and closely adheres to all constraints. The complete code listing is provided at the end of this article.

Happy Computing,

Paul Shirkey

References, Resources, Notes

[0] Due to the size of this QP problem and the number of constraints (227) the current release of NMath's ActiveSetQPSolver() fails to correctly find the optimal portfolio. However, the next release of NMath due in May (NMath 6.0) includes a major upgrade to many of our LP, QP, and NLP classes. Many of these classes in NMath 6.0 are backed by the Microsoft Solver Foundation, providing the ability to solve much larger problems correctly and efficiently.

[1] The port5 data set can be found at http://people.brunel.ac.uk/~mastjjb/jeb/orlib/files/port5.txt . This data set is part of the OR-Library, a set of standard data sets maintained by J. E. Beasley at http://people.brunel.ac.uk/~mastjjb/jeb/info.html.

[2] This blog note follows the notation of this clearly written paper, by Paul J. Atzberger, on optimal portfolio allocation, variants, and the efficient frontier: http://www.math.ucsb.edu/~atzberg/finance/portfolioTheory.pdf.

[3] Chang, T.-J., Meade, N., Beasley, J.E. and Sharaiha, Y.M., "Heuristics for cardinality constrained portfolio optimisation" Comp. & Opns. Res. 27 (2000) 1271-1302.

[4] MATLAB uses this same data set in their optimization documentation.

[5] Markowitz, H.M. (March 1952). "Portfolio Selection". The Journal of Finance 7 (1): 77–91. [paper in pdf]

.NET Code Listings

Full QP solution code. Note that NMath 6.0 (due May 2014) is required.

using System;
using CenterSpace.NMath.Core;  
using CenterSpace.NMath.Analysis;
using CenterSpace.NMath.Charting.Microsoft;
using System.Windows.Forms.DataVisualization.Charting;

public void OptimalPortAllocation()
    {
      // Get port5 data set : http://people.brunel.ac.uk/~mastjjb/jeb/orlib/files/port5.txt
      // File Format of port5:
      // Line 1: Text description of data
      // Line 2: number of assets, N
      // Line 2 - 2+N : list of mean return _ standard return
      // Remaining 1/2 N*N lines: correlation matrix between asset i and j
      FloatVector meanReturn = null ;
      FloatVector stdDevReturn = null;
      FloatMatrix correlation = null;
      int n = loadData( ref meanReturn, ref stdDevReturn, ref correlation );

      double targetReturn = 0.002;

      // Set up QR problem using port5.txt data
      FloatMatrix covariance = correlation * ( NMathFunctions.Product( new FloatMatrix( stdDevReturn ), ( new FloatMatrix( stdDevReturn ).Transpose() ) ) );
      QuadraticProgrammingProblem problem = new QuadraticProgrammingProblem();
      problem.H = covariance;
      problem.c = new DoubleVector(n, 0);

      // Set up constraints
      LinearConstraint sumToOne = new LinearConstraint( new DoubleVector( n, 1 ), 1, ConstraintType.EqualTo );
      LinearConstraint returnRate = new LinearConstraint( meanReturn, targetReturn, ConstraintType.GreaterThanOrEqualTo );
      problem.AddConstraint( returnRate );
      problem.AddConstraint( sumToOne );

      // Add the bound on each var, w: w > 0
      for ( int i = 0; i < n; i++ )
        problem.AddLowerBound( i, 0.0 );
   
      // Solve constrainted QP
      var solver = new ActiveSetQPSolver();
      solver.StepSizeEpsilon = 1e-10;

      var startEqualAllocation = new DoubleVector( n, 1.0 / n );
      var optAllocation = new DoubleVector();
      
      long before = DateTime.Now.Ticks;
      if ( solver.Solve( problem, startEqualAllocation ) )
      {
        optAllocation = solver.OptimalX;
      }
      else
      {
        throw new Exception( "Solve failed to find a solution." );
      }
      long after = DateTime.Now.Ticks;
      long ticks = after - before;
      double millis = ( (double) ticks ) / 10000;

      Console.WriteLine("Asset #    Allocation");
      double wealth = 0.0;
      double measuredReturnRate = 0.0;
      for ( int i = 0; i < optAllocation.Length; i++ )
      {
        if ( optAllocation[i] > 0.0000001 )
        {
          Console.WriteLine( String.Format( "{0,4},  {1,7:0.0000}",i, optAllocation[i]));
          wealth += optAllocation[i];
          measuredReturnRate += optAllocation[i] * meanReturn[i];
        }

      }
      Console.WriteLine(String.Format("Total allocation: {0,7:0.0000}", wealth) );
      Console.WriteLine( String.Format( "Total return rate: {0,7:0.0000}%, Target return rate {1,7:0.0000}%", 100 * measuredReturnRate, 100 * targetReturn ) );
      Console.WriteLine( String.Format( "Total solver time required: {0,7:0.0000} seconds", millis/1000 ) );


      // Chart optimal portfolio allocation
      DoubleVector x = new DoubleVector(n, 0, 1);
      DoubleVector w = optAllocation;
      var chart = NMathChart.ToChart( x, w );
      chart.Series[0].MarkerStyle = MarkerStyle.Square;
      chart.Series[0].ChartType = SeriesChartType.Bar;
      NMathChart.Show( chart );

    }

Below is the full parsing code for the port5.txt data file.

    private int loadData( ref FloatVector meanReturn, ref FloatVector stdDevReturn, ref FloatMatrix correlation )
    {
      int n;

      // Fix up the path here to point to your data file copy.
      using ( StreamReader file = new StreamReader( "./data/PortfolioOptimzation_port5.data.txt" ) )
      {
        file.ReadLine(); // skip first line of explanatory text
        n = Int32.Parse( file.ReadLine() );

        // Now get the next n mean return and standard return values.
        meanReturn = new FloatVector( n );
        stdDevReturn = new FloatVector( n );
        string[] values = new string[3];
        for ( int k = 0; k < n; k++ )
        {
          values = file.ReadLine().Split( ' ' );
          meanReturn[k] = float.Parse( values[1] );
          stdDevReturn[k] = float.Parse( values[2] );
        }

        // Now get the correlation matrix.
        correlation = new FloatMatrix( n, n );
        int cnt = 0;
        for ( int i = cnt; i < n; i++ )
        {
          for ( int j = cnt; j < n; j++ )
          {
            values = file.ReadLine().Split( ' ' );
            correlation[i, j] = float.Parse( values[3] );
            correlation[j, i] = float.Parse( values[3] );
          }

          cnt++;
        }
      }
      return n;
    }

Optimization with Markowitz Theory

Solving the Quadratic Programming Problem

References, Resources, Notes

.NET Code Listings

Leave a Reply