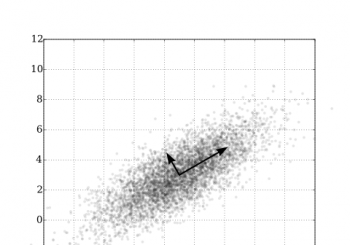
Principal Components Regression: Recap of Part 2
Recall that the least squares solution to the multiple linear problem is given by(1) $latex \hat{\beta} = (X^T X)^{-1} X^T y $
And that problems occurred finding when the matrix(2)
was close to being singular. The Principal Components Regression approach to addressing the problem is to replace in equation (1) with a better conditioned...
Read More
Read More
